题目内容
(1)解方程:
(2)如图,△ABC各顶点的坐标分别为A(4、4),B(-2,2),C(3,0),
①画出它的以原点O为对称中心的△AˊBˊCˊ
②写出 Aˊ,Bˊ,Cˊ三点的坐标。

(3)已知关于x的方程mx2-(m+2)x+2=0(m≠0).
①求证:方程总有两个实数根;
②若方程的两个实数根都是整数,求正整数m的值.
(1)x1= ,x2=-
,x2=- .(2)作图见解析;(3)①证明见解析,②1或2.
.(2)作图见解析;(3)①证明见解析,②1或2.
【解析】
试题分析:(1) 首先将二次项系数化为1.然后移项,把常数项移到等号的右边,方程左右两边同时加上一次项系数一半的平方,则左边是完全平方式,右边是常数项,即可直接开方求解.
(2)①根据网格结构特点分别找出点A、B、C关于原点对称的点的位置,然后顺次连接即可;
②根据平面直角坐标系写出各点坐标即可.
(3)(1)先计算判别式的值得到△=(m+2)2-4m×2=(m-2)2,再根据非负数的值得到△≥0,然后根据判别式的意义得到方程总有两个实数根;
(2)利用因式分解法解方程得到x1=1,x2= ,然后利用整数的整除性确定正整数m的值.
,然后利用整数的整除性确定正整数m的值.
试题解析:(1) 原式两边都除以6,移项得x2- x=2,
x=2,
配方,得x2- x+(-
x+(- )2=2+(-
)2=2+(- )2,
)2,
(x- )2=(
)2=( )2,
)2,
即x- =
= 或x-
或x- =-
=- ,
,
所以x1= ,x2=-
,x2=- .
.
(2)①△AˊBˊCˊ如图所示;

②Aˊ(-4,-4),Bˊ(2,-2),Cˊ(-3,0)
(3)(1)证明:∵m≠0,
△=(m+2)2-4m×2
=m2-4m+4
=(m-2)2,
而(m-2)2≥0,即△≥0,
∴方程总有两个实数根;
(2)【解析】
(x-1)(mx-2)=0,
x-1=0或mx-2=0,
∴x1=1,x2= ,
,
当m为正整数1或2时,x2为整数,
即方程的两个实数根都是整数,
∴正整数m的值为1或2.
考点:1.解一元二次方程-配方法;2.作图旋转变换;3.根的判别式.

 名校课堂系列答案
名校课堂系列答案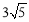 ,tan∠CPO=
,tan∠CPO=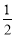 ,求弦CD的长.
,求弦CD的长.
 B.3 C.
B.3 C. D.
D.
 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,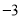 ).[图(2)为解答备用图]
).[图(2)为解答备用图]
 __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________; 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
 (k≠0)的图象经过点P(﹣2,3),则该函数的图象不经过的点是( )
(k≠0)的图象经过点P(﹣2,3),则该函数的图象不经过的点是( ) 的值.
的值.