题目内容
如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.

(1)求证:△EBF∽△FCD;
(2)连接DH,如果BC=12,BF=3,求tan∠HDG的值.
(1)证明见试题解析;(2)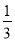 .
.
【解析】
试题分析:(1)由正方形的性质得到∠B=∠C=90°,∠EFG=90°,BC=CD,GH=EF=FG.由∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,得到 ∠EFB =∠FDC.故△EBF∽△FCD;
(2)在Rt△CDF中,由勾股定理得到DF的长,由△EBF∽△FCD,得到 BE的长,再由勾股定理得到GH=的长,由于DG=DF-FG=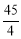 ,故可得到 tan∠HDG的值.
,故可得到 tan∠HDG的值.
试题解析:(1)证明:∵ 正方形ABCD,正方形EFGH,∴ ∠B=∠C=90°,∠EFG=90°,BC=CD,GH=EF=FG.又∵ 点F在BC上,点G在FD上,

 ∴ ∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,∴ ∠EFB =∠FDC.∴ △EBF∽△FCD;
∴ ∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,∴ ∠EFB =∠FDC.∴ △EBF∽△FCD;
(2)【解析】
∵ BF=3,BC=CD=12,
 ∴ CF=9,DF=
∴ CF=9,DF=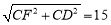 ,由(1)得
,由(1)得 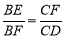 ,∴ BE=
,∴ BE=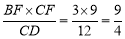 ,∴GH=FG=EF=
,∴GH=FG=EF=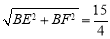 ,DG=DF-FG=
,DG=DF-FG=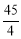 ,∴ tan∠HDG=
,∴ tan∠HDG=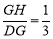 .
.
考点:1.正方形的性质;2.相似三角形的判定与性质;3.解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
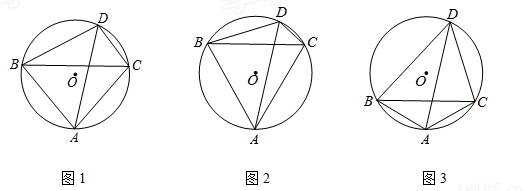
 ,直接写出∠ADB的大小(用含
,直接写出∠ADB的大小(用含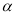 的式子表示);
的式子表示); BAC=60°,求证:BD+CD=AD;
BAC=60°,求证:BD+CD=AD;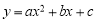 的图象如图所示,则下列结论中错误的是( )
的图象如图所示,则下列结论中错误的是( )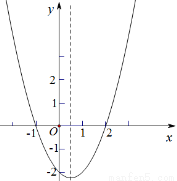
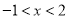 时,
时,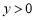
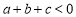
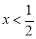 ,y随x的增大而减小
,y随x的增大而减小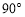 的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为
的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为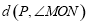 .
.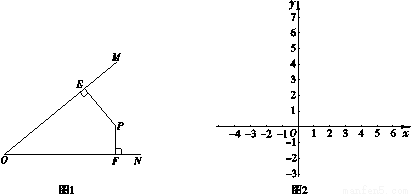
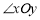 ,点P为第一象限内或两条坐标轴正半轴上的动点,且满足
,点P为第一象限内或两条坐标轴正半轴上的动点,且满足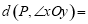 5,点P运动形成的图形记为图形G.
5,点P运动形成的图形记为图形G.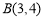 ,
,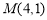 ,求
,求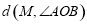 的值;
的值;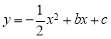 经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当
经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当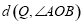 取最大值时,点Q 的坐标.
取最大值时,点Q 的坐标.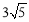 ,tan∠CPO=
,tan∠CPO=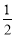 ,求弦CD的长.
,求弦CD的长.
 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )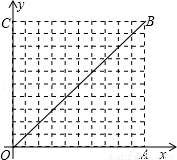

 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,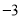 ).[图(2)为解答备用图]
).[图(2)为解答备用图]
 __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________; 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;