题目内容
如果|m-3|+(n+2)2=0,则方程3mx+1=x+n的解是 .
考点:解一元一次方程,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:根据绝对值和平方数都≥0即可求得m、n的值,解一元一次方程即可解题.
解答:解:∵|m-3|+(n+2)2=0,
∴m=3,n=-2,
原方程3mx+1=x+n为9x+1=x-2,
解得x=-
.
∴m=3,n=-2,
原方程3mx+1=x+n为9x+1=x-2,
解得x=-
| 3 |
| 8 |
点评:本题考查了绝对值和偶次方都是非负数的性质,考查了移项、合并同类项求一元一次方程的解的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
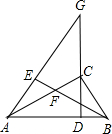 如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,G是DC延长线上一点,过B作BE⊥AG,垂足为E,交CD于点F.求证:CD2=DF•DG.
如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,G是DC延长线上一点,过B作BE⊥AG,垂足为E,交CD于点F.求证:CD2=DF•DG.