题目内容
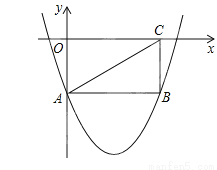
如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)
练习册系列答案
相关题目


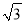 米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)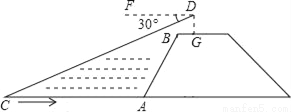
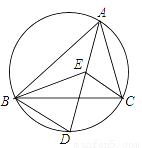
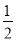 AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.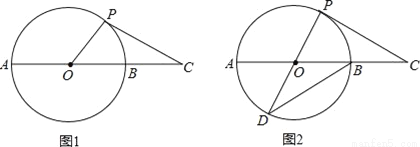
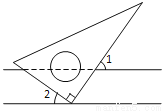
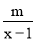 =l的解是非负数,则m的取值范围是( )
=l的解是非负数,则m的取值范围是( )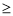 l B. m
l B. m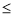 l C. m
l C. m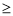 -l旦m≠0 D. m
-l旦m≠0 D. m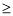 -l
-l