题目内容
14．已知：直线m经过点O，点A在直线m外，且OA=2，记点A到直线m的距离为d，试写出d的取值范围．分析 由于点A在直线m外，所以OA和直线m有两种可能：①垂直相交，此时d=AO；②不垂直相交，此时d＜AO．由此即可确定d的取值范围．
解答 解：∵当Ao⊥直线m时，O为垂足，此时d=AO=2，
∴0＜d≤2．
点评 此题主要考查了平面内直线的位置关系、点的直线的距离等知识，利用点的直线的距离可以确定点A到直线m的距离的范围．
练习册系列答案
阅读快车系列答案
相关题目
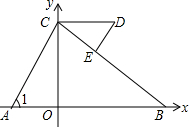如图，平面直角坐标系中，C（0，5）、D（a，5）（a＞0），A、B在x轴上，∠1=∠D，请写出∠ACB和∠BED数量关系以及证明．
如图所示，在Rt△ABC中，∠C=90°，∠BAC、∠ABC的平分线相交于点D，且DE⊥BC于点E，DF⊥AC于点F，那么四边形CEDF是正方形吗？请说明理由（提示：可作DG⊥AB于点G）
如图，在正方形ABCD中，两条对角线相交于点O，∠BCA的平分线交BD于E，若正方形ABCD的周长为12cm，则BE=1cm．
19．化简$\frac{ab-b}{{a}^{2}-2a+1}$的结果是（ ）
| A． | $\frac{a}{a+1}$ | B． | $\frac{a}{a-1}$ | C． | $\frac{b}{a+1}$ | D． | $\frac{b}{a-1}$ |