题目内容
17．若4sin2A-4sinAcosA+cos2A=0，则tanA=$\frac{1}{2}$．分析 先解一元二次方程，再根据锐角三角函数的定义得出即可．
解答 解：4sin2A-4sinAcosA+cos2A=0，
（2sinA-cosA）2=0，
2sinA-cosA=0，
2sinA=cosA，
tanA=$\frac{sinA}{cosA}$=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$
点评 本题考查了锐角三角函数的定义和解一元二次方程等知识点，比较简单，注意锐角三角函数定义的掌握．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
如图，点P在边长为1的正方形ABCD边AD上，连接PB．过点B作一条射线与边DC的延长线交于点Q，使得∠QBE=∠PBC，其中E是边AB延长线上的点，连接PQ．若PQ2=PB2+PD2+1，则△PAB的面积为$\frac{1}{4}$．
5．
如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为（ ）
如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为（ ）| A． | 4$\sqrt{5}$cm | B． | 3$\sqrt{5}$cm | C． | 5$\sqrt{5}$cm | D． | 4cm |
如图，∠ABD=∠ACD，∠ADB=90°-$\frac{1}{2}$∠BDC，求证：△ABC是等腰三角形．
如图，在3×1的方格纸中，试求∠ACB+∠AFB+∠AEB的度数，并说明理由．
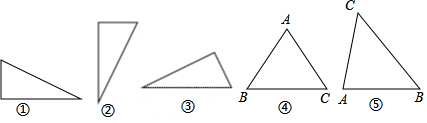
6．Word文本中的图形，在图形格式中大小菜单下显示有图形的绝对高度和绝对宽度，同一个图形随其放置方向的变化，所显示的绝对高度和绝对宽度也随之变化．如图①、②、③是同一个三角形以三条不同的边水平放置时，它们所显示的绝对高度和绝对宽度如下表，现有△ABC，已知AB=AC，当它以底边BC水平放置时（如图④），它所显示的绝对高度和绝对宽度如下表，那么当△ABC以腰AB水平放置时（如图⑤），它所显示的绝对高度和绝对宽度分别是（ ）
| 图形 | 图① | 图② | 图③ | 图④ | 图⑤ |
| 绝对高度 | 1.50 | 2.00 | 1.20 | 2.40 | ？ |
| 绝对宽度 | 2.00 | 1.50 | 2.50 | 3.60 | ？ |
| A． | 3.60和2.40 | B． | 2.56和3.00 | C． | 2.56和2.88 | D． | 2.88和3.00 |