题目内容
 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,则点C2坐标为
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,则点C2坐标为
- A.

- B.

- C.

- D.

D
分析:证明△DOA∽△ABA1,则可求出A1B,由△ABA1∽△A1B1A2,可得出B1A2,从而可得出第一、第二、第三个正方形的边长,过点DE作x轴的平行线,过点C2作C2F⊥DE于点F,在Rt△DC2F中求出DF,C2F,从而可得出C2坐标.
解答:∵OD=2,OA=1,
∴AD=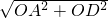 =
= ,
,
∵∠BAA1+∠OAD=90°,∠ODA=∠BAA1,
∴∠BAA1=∠ODA,
∴△DOA∽△ABA1,
∴ =
= ,即
,即 =
= ,
,
解得:BA1= ,
,
∴CA1=CB+BA1=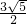 ,
,
由△ABA1∽△A1B1A2,可得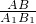 =
= ,即
,即 =
= ,
,
解得:B1A2=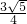 ,
,
∴C1A2=CB1+B1A2=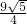 ,
,
过点DE作x轴的平行线,过点C2作C2F⊥DE于点F,

则易得∠C2DF=∠ODA,
∴sin∠C2DF=sin∠ODA=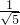 =
= =
= ,
,
解得:C2F= ,
,
∴tan∠C2DF=tan∠ODA= =
= =
= ,
,
解得:DF= ,
,
∴可得C2的横坐标为 ,纵坐标为
,纵坐标为 +2=
+2= .
.
即点C2的坐标为( ,
, ).
).
故选D.
点评:本题考查了相似三角形的判定与性质,解答本题的关键是根据相似三角形的对应边成比例,求出前三个正方形的边长,有一定难度,注意耐心思考.
分析:证明△DOA∽△ABA1,则可求出A1B,由△ABA1∽△A1B1A2,可得出B1A2,从而可得出第一、第二、第三个正方形的边长,过点DE作x轴的平行线,过点C2作C2F⊥DE于点F,在Rt△DC2F中求出DF,C2F,从而可得出C2坐标.
解答:∵OD=2,OA=1,
∴AD=
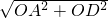 =
= ,
,∵∠BAA1+∠OAD=90°,∠ODA=∠BAA1,
∴∠BAA1=∠ODA,
∴△DOA∽△ABA1,
∴
 =
= ,即
,即 =
= ,
,解得:BA1=
 ,
,∴CA1=CB+BA1=
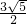 ,
,由△ABA1∽△A1B1A2,可得
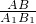 =
= ,即
,即 =
= ,
,解得:B1A2=
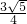 ,
,∴C1A2=CB1+B1A2=
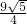 ,
,过点DE作x轴的平行线,过点C2作C2F⊥DE于点F,

则易得∠C2DF=∠ODA,
∴sin∠C2DF=sin∠ODA=
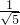 =
= =
= ,
,解得:C2F=
 ,
,∴tan∠C2DF=tan∠ODA=
 =
= =
= ,
,解得:DF=
 ,
,∴可得C2的横坐标为
 ,纵坐标为
,纵坐标为 +2=
+2= .
.即点C2的坐标为(
 ,
, ).
).故选D.
点评:本题考查了相似三角形的判定与性质,解答本题的关键是根据相似三角形的对应边成比例,求出前三个正方形的边长,有一定难度,注意耐心思考.

练习册系列答案
相关题目
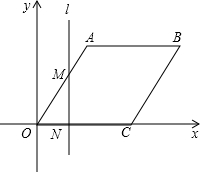

 例函数图象上的点P,使得四边形PGMC′是平行四边形?如果存在,请求出点M和点P的坐标;如果不存在,请说明理由.
例函数图象上的点P,使得四边形PGMC′是平行四边形?如果存在,请求出点M和点P的坐标;如果不存在,请说明理由.
 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC