题目内容
(2013•湖州二模)如图,在平面直角坐标系中,直线y=kx和双曲线y=
在第一象限相交于点A(1,2),点B在y轴上,且AB⊥y轴.有一动点P从原点出发沿y轴以每秒1个单位的速度向y轴的正方向运动,运动时间为t秒(t>0),过点P作PD⊥y轴,交直线OA于点C,交双曲线于点D.

(1)求直线y=kx和双曲线y=
的函数关系式;
(2)设四边形CDAB的面积为S,当P在线段OB上运动时(P不与B点重合),求S与t之间的函数关系式;
(3)在图中第一象限的双曲线上是否存在点Q,使以A、B、C、Q四点为顶点的四边形是平行四边形?若存在,请求出此时t的值和Q点的坐标;若不存在,请说明理由.
| k′ |
| x |

(1)求直线y=kx和双曲线y=
| k′ |
| x |
(2)设四边形CDAB的面积为S,当P在线段OB上运动时(P不与B点重合),求S与t之间的函数关系式;
(3)在图中第一象限的双曲线上是否存在点Q,使以A、B、C、Q四点为顶点的四边形是平行四边形?若存在,请求出此时t的值和Q点的坐标;若不存在,请说明理由.
分析:(1)把A的坐标代入正比例函数与反比例函数的解析式,;利用待定系数法即可求得函数的解析式;
(2)OP=t,把y=t代入正比例函数与反比例函数的解析式,求得C,D的横坐标,则CD的长即可利用t表示出来,然后利用梯形的面积公式即可写出函数的解析式;
(3)分AB=∥CD,且CD在AB下方时;当AB=∥CD,且CD在AB上方时以及BQ=∥AC,且CD在AB下方三种情况进行讨论.依据一组对边平行且相等的四边形是平行四边形即可求解.
(2)OP=t,把y=t代入正比例函数与反比例函数的解析式,求得C,D的横坐标,则CD的长即可利用t表示出来,然后利用梯形的面积公式即可写出函数的解析式;
(3)分AB=∥CD,且CD在AB下方时;当AB=∥CD,且CD在AB上方时以及BQ=∥AC,且CD在AB下方三种情况进行讨论.依据一组对边平行且相等的四边形是平行四边形即可求解.
解答: 解:(1)把A(1,2)代入y=kx和y=
解:(1)把A(1,2)代入y=kx和y=
,得
K=2,k?=2
∴直线y=kx的函数关系式是y=2x
双曲线y=
的函数关系式是y=
,
(2)∵AB=1,OB=2,OP=t
∴PC=
,PD=
,BP=2-t
∴当CD在AB下方时,CD=PD-PC=
-
.
∴S=
(1+
-
)(2-t)
=
(0<t<2),
(注:自变量t的取值范围没有写出的不扣分,函数化简结果可以用不同
的形式表示,只要结果正确的均不扣分,如:S=
-t+
等)
(3)存在3种情形,具体如下:
①当AB=∥CD,且CD在AB下方时(图2)
CD=PD-PC=
-
=1,
解得 t1=
-1,t2=-
-1(舍去)
∴PD=
=
=
,OP=t=
-1
∴当t=
-1时,存在Q(
,
-1)使以
A、B、C、Q四点为顶点的四边形是平行四边形,
②当AB=∥CD,且CD在AB上方时(图2)
CD=PC-PD=
-
=1,解得 t1=
+1,t2=-
+1(舍去)
∴PD=
=
=
,OP=t=
+1
∴当t=
+1时,存在Q(
,
+1)使以
A、B、C、Q四点为顶点的四边形是平行四边形,
③当BQ=∥AC,且CD在AB下方时(见图3)
此时Q点的坐标仍为(
,
+1)
过C作CG⊥AB交AB于G,
过Q作QH⊥y轴交y轴于H
显然,△ACG≌△QBH
∴CG=BH=BP
∴OP=2OB-OH=4-(
+1)=3-
∴当t=3-
时,存在Q(
,
+1)使以A、B、C、Q四点为顶点的四边形是平行四边形.
 解:(1)把A(1,2)代入y=kx和y=
解:(1)把A(1,2)代入y=kx和y=| k′ |
| x |
K=2,k?=2
∴直线y=kx的函数关系式是y=2x
双曲线y=
| k′ |
| x |
| 2 |
| x |
(2)∵AB=1,OB=2,OP=t
∴PC=
| t |
| 2 |
| 2 |
| t |
∴当CD在AB下方时,CD=PD-PC=
| 2 |
| t |
| t |
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
| t |
| t |
| 2 |
=
| t3-4t2+8 |
| 4t |
(注:自变量t的取值范围没有写出的不扣分,函数化简结果可以用不同
的形式表示,只要结果正确的均不扣分,如:S=
| t2 |
| 4 |
| 2 |
| t |
(3)存在3种情形,具体如下:
①当AB=∥CD,且CD在AB下方时(图2)
CD=PD-PC=
| 2 |
| t |
| t |
| 2 |
解得 t1=
| 5 |
| 5 |
∴PD=
| 2 |
| t |
| 2 | ||
|
| ||
| 2 |
| 5 |
∴当t=
| 5 |
| ||
| 2 |
| 5 |
A、B、C、Q四点为顶点的四边形是平行四边形,

②当AB=∥CD,且CD在AB上方时(图2)
CD=PC-PD=
| t |
| 2 |
| 2 |
| t |
| 5 |
| 5 |
∴PD=
| 2 |
| t |
| 2 | ||
|
| ||
| 2 |
| 5 |
∴当t=
| 5 |
| ||
| 2 |
| 5 |
A、B、C、Q四点为顶点的四边形是平行四边形,
③当BQ=∥AC,且CD在AB下方时(见图3)
此时Q点的坐标仍为(
| ||
| 2 |
| 5 |

过C作CG⊥AB交AB于G,
过Q作QH⊥y轴交y轴于H
显然,△ACG≌△QBH
∴CG=BH=BP
∴OP=2OB-OH=4-(
| 5 |
| 5 |
∴当t=3-
| 5 |
| ||
| 2 |
| 5 |
点评:本题是待定系数法求函数解析式,平行四边形的判定方法的综合应用,正确理解分情况讨论是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
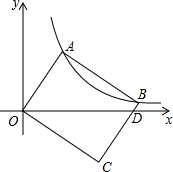 (2013•湖州二模)如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=
(2013•湖州二模)如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y= (2013•湖州二模)如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=25°,那么∠2的度数是( )
(2013•湖州二模)如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=25°,那么∠2的度数是( )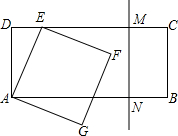 (2013•湖州二模)如图,矩形ABCD中,AB=8,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG.同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过多少秒时.直线MN和正方形AEFG开始有公共点?( )
(2013•湖州二模)如图,矩形ABCD中,AB=8,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG.同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过多少秒时.直线MN和正方形AEFG开始有公共点?( )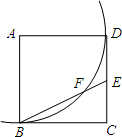 (2013•湖州二模)如图,点E是正方形ABCD的边CD上一点,以A为圆心,AB为半径的弧与BE交于点F,则∠EFD=
(2013•湖州二模)如图,点E是正方形ABCD的边CD上一点,以A为圆心,AB为半径的弧与BE交于点F,则∠EFD=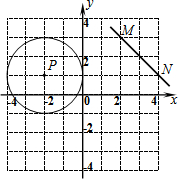 (2013•湖州二模)如图,⊙P与y轴相切,圆心为P(-2,1),直线MN过点M(2,3),N(4,1).
(2013•湖州二模)如图,⊙P与y轴相切,圆心为P(-2,1),直线MN过点M(2,3),N(4,1).