题目内容
（2012•绥化）如图，四边形ABCD为矩形，C点在x轴上，A点在y轴上，D点坐标是（0，0），B点
坐标是（3，4），矩形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD、AB上，且F点的坐标是（2，4）．
（1）求G点坐标；
（2）求直线EF解析式；
（3）点N在x轴上，直线EF上是否存在点M，使以M、N、F、G为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．
坐标是（3，4），矩形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD、AB上，且F点的坐标是（2，4）．（1）求G点坐标；
（2）求直线EF解析式；
（3）点N在x轴上，直线EF上是否存在点M，使以M、N、F、G为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．
分析：（1）根据折叠性质可知FG=AF=2，而FB=AB-AF=1，则在Rt△BFG中，利用勾股定理求出BG的长，从而得到CG的长，从而得到G点坐标；
（2）由题意，可知△AEF为含30度角的直角三角形，从而可求出E点坐标；又F点坐标已知，所以可利用待定系数法求出直线EF的解析式；
（3）本问关键是确定平行四边形的位置与形状．因为M、N均为动点，只有FG已经确定，所以可从此入手，按照FG为一边、FG为对角线的思路，顺序探究可能的平行四边形的形状．确定平行四边形的位置与形状之后，利用全等三角形求得M点的纵坐标，再利用直线解析式求出M点的横坐标，从而求得M点的坐标．
（2）由题意，可知△AEF为含30度角的直角三角形，从而可求出E点坐标；又F点坐标已知，所以可利用待定系数法求出直线EF的解析式；
（3）本问关键是确定平行四边形的位置与形状．因为M、N均为动点，只有FG已经确定，所以可从此入手，按照FG为一边、FG为对角线的思路，顺序探究可能的平行四边形的形状．确定平行四边形的位置与形状之后，利用全等三角形求得M点的纵坐标，再利用直线解析式求出M点的横坐标，从而求得M点的坐标．
解答：解：（1）由已知得，FG=AF=2，FB=1
∵四边形ABCD为矩形
∴∠B=90°
BG=
=
=
∴G点的坐标为（3，4-
）；
（2）设直线EF的解析式是y=kx+b
在Rt△BFG中，cos∠BFG=
=
∴∠BFG=60°
∴∠AFE=∠EFG=60°
∴AE=AFtan∠AFE=2tan60°=2
∴E点的坐标为（0，4-2
）
又F点的坐标是（2，4）
∴
解得k=
，b=4-2
；
∴直线EF的解析式为y=
x+4-2
；
注：
求E点坐标方法二：过点E作EP⊥BC于点P，利用△BFG∽△PGE得到OE=4-2
，所以E（0，4-2
）；
求E点坐标方法三：过点E作EP⊥BC于点P，在Rt△GEP中，由勾股定理得EG2=GP2+EP2，得到OE=4-2
，所以E（0，4-2
）；
求E点坐标方法四：连接AG，证△AEG是等边三角形，得到OE=4-2
，所以E（0，4-2
）．
（3）若以M、N、F、G为顶点的四边形是平行四边形，则可能存在以下情形：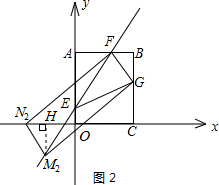
①FG为平行四边形的一边，且N点在x轴正半轴上，如图1所示．
过M1点作M1H⊥x轴于点H，
∵M1N1∥FG，
∴∠HN1M1=∠HQF，
又∵AB∥OQ，
∴∠HQF=∠BFG，
∴∠HN1M1=∠BFG
又∵∠M1HN1=∠B=90°，M1N1=FG，
∴△M1HN1≌△GBF，
∴M1H=GB=
，即yM1=
．
由直线EF解析式y=
x+4-2
，求出xM1=3-
．
∴M1（3-
，
）；
②FG为平行四边形的一边，且N点在x轴负半轴上，如图2所示．
仿照与①相同的办法，可求得M2（1-
，-
）；
③FG为平行四边形的对角线，如图3所示．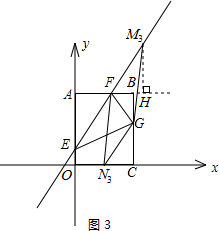
过M3作FB延长线的垂线，垂足为H．易证△M3FH≌△GN3C，则有M3H=CG=4-
，所以M3的纵坐标为8-
；
代入直线EF解析式，得到M3的横坐标为1+
．
∴M3（1+
，8-
）．
综上所述，存在点M，使以M、N、F、G为顶点的四边形是平行四边形．
点M的坐标为：M1（3-
，
），M2（1-
，-
），M3（1+
，8-
）．
∵四边形ABCD为矩形
∴∠B=90°
BG=
| FG2-FB2 |
| 22-12 |
| 3 |
∴G点的坐标为（3，4-
| 3 |
（2）设直线EF的解析式是y=kx+b
在Rt△BFG中，cos∠BFG=
| FB |
| FG |
| 1 |
| 2 |
∴∠BFG=60°
∴∠AFE=∠EFG=60°
∴AE=AFtan∠AFE=2tan60°=2
| 3 |
∴E点的坐标为（0，4-2
| 3 |
又F点的坐标是（2，4）
∴
|
解得k=
| 3 |
| 3 |
∴直线EF的解析式为y=
| 3 |
| 3 |
注：
求E点坐标方法二：过点E作EP⊥BC于点P，利用△BFG∽△PGE得到OE=4-2
| 3 |
| 3 |
求E点坐标方法三：过点E作EP⊥BC于点P，在Rt△GEP中，由勾股定理得EG2=GP2+EP2，得到OE=4-2
| 3 |
| 3 |
求E点坐标方法四：连接AG，证△AEG是等边三角形，得到OE=4-2
| 3 |
| 3 |
（3）若以M、N、F、G为顶点的四边形是平行四边形，则可能存在以下情形：
①FG为平行四边形的一边，且N点在x轴正半轴上，如图1所示．
过M1点作M1H⊥x轴于点H，
∵M1N1∥FG，
∴∠HN1M1=∠HQF，
又∵AB∥OQ，
∴∠HQF=∠BFG，
∴∠HN1M1=∠BFG
又∵∠M1HN1=∠B=90°，M1N1=FG，
∴△M1HN1≌△GBF，
∴M1H=GB=
| 3 |
| 3 |
由直线EF解析式y=
| 3 |
| 3 |
4
| ||
| 3 |
∴M1（3-
4
| ||
| 3 |
| 3 |
②FG为平行四边形的一边，且N点在x轴负半轴上，如图2所示．
仿照与①相同的办法，可求得M2（1-
4
| ||
| 3 |
| 3 |
③FG为平行四边形的对角线，如图3所示．
过M3作FB延长线的垂线，垂足为H．易证△M3FH≌△GN3C，则有M3H=CG=4-
| 3 |
| 3 |
代入直线EF解析式，得到M3的横坐标为1+
4
| ||
| 3 |
∴M3（1+
4
| ||
| 3 |
| 3 |
综上所述，存在点M，使以M、N、F、G为顶点的四边形是平行四边形．
点M的坐标为：M1（3-
4
| ||
| 3 |
| 3 |
4
| ||
| 3 |
| 3 |
4
| ||
| 3 |
| 3 |
点评：本题考查了直角坐标系中一次函数与平面图形的性质，涉及到的考点包括待定系数法求一次函数（直线）解析式、矩形、平行四边形、直角三角形、全等三角形的判定与性质、勾股定理等，对解题能力要求较高．难点在于第（3）问，这是一个存在性问题，注意平行四边形有三种可能的情形，需要一一分析并求解，避免遗漏．
练习册系列答案
相关题目
（2012•绥化）如图，点A、B、C、D为⊙O的四等分点，动点P从圆心O出发，沿OC-
（2012•绥化）如图，二次函数y=ax2-4x+c的图象经过坐标原点，与x轴交于点A（-4，0）．
格点，△ABC的顶点均在格点上，O、M也在格点上．
（2012•绥化）如图，AB∥ED，∠ECF=70°，则∠BAF的度数为（ ）