题目内容
14．在Rt△ABC中，∠C=90°，AC=9，AB=15，则点C到AB的距离是（ ）| A． | $\frac{36}{5}$ | B． | 12 | C． | 9 | D． | $\frac{3\sqrt{3}}{4}$ |
分析 首先根据勾股定理求出直角边BC的长，再根据三角形的面积为定值即可求出则点C到AB的距离．
解答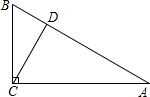 
解：在Rt△ABC中，∠C=90°，则有AC2+BC2=AB2，
∵AC=9，BC=12，
∴AB=解：在Rt△ABC中，∠C=90°，则有AC2+BC2=AB2，
∵AC=9，AB=15，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=12，
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•h，
∴h=$\frac{12×9}{15}$=$\frac{36}{5}$．
故选A．
点评 本题考查了勾股定理在直角三角形中的应用，解本题的关键是正确的运用勾股定理，确定AB为斜边．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
4．下列运算中，正确的是（ ）
| A． | 3x+2x2=5x2 | B． | 2a2b-a2b=1 | C． | （-6）+（-2）=-3 | D． | （-$\frac{2}{3}$）2=$\frac{4}{9}$ |
2．下列几个命题中：
①|-5|的算术平方根是5；
②数据7、1、3、5、6、3的中位数是3，众数是4；
③对顶角相等；
④点P（1，-2）关于x轴的对称点在第三象限，
其中真命题的个数是（ ）
①|-5|的算术平方根是5；
②数据7、1、3、5、6、3的中位数是3，众数是4；
③对顶角相等；
④点P（1，-2）关于x轴的对称点在第三象限，
其中真命题的个数是（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
9．阅读：在直线上有n个不同的点，则此图中共有多少条线段？通过分析、画图尝试得如下表格：
问题：
（1）把表格补充完整；
（2）根据上述得到的信息解决下列问题：
①某学校七年级共有20个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛共要进行多少场？
②乘火车从A站出发，沿途经过10个车站方可到达B站，那么在A，B两站之间需要安排多少种不同的车票？
| 图形 | 直线上点的个数 | 共有线段的条数 | 两者关系 |
 | 2 | 1 | 0+1=$\frac{2×（2-1）}{2}$=1 |
 | 3 | 3 | 0+1+2=$\frac{3×（3-1）}{2}$=3 |
 | 4 | 6 | 0+1+2+3=$\frac{4×（4-1）}{2}$=6 |
| … | … | … | … |
 | n |
（1）把表格补充完整；
（2）根据上述得到的信息解决下列问题：
①某学校七年级共有20个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛共要进行多少场？
②乘火车从A站出发，沿途经过10个车站方可到达B站，那么在A，B两站之间需要安排多少种不同的车票？
已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点的坐标分别为（-1，0），（3，0）．对于下列结论：①abc＞0，；b2-4ac＞0；③当x1＜x2＜0时，y1＞y2；④当-1＜x＜3时，y＞0．其中正确的有①②③个．
3．把等式ad=bc写成比例式，下列写法错误的是（ ）
| A． | $\frac{a}{b}$=$\frac{c}{d}$ | B． | $\frac{a}{c}$=$\frac{b}{d}$ | C． | $\frac{c}{a}$=$\frac{d}{b}$ | D． | $\frac{a}{d}$=$\frac{b}{c}$ |