题目内容
国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A,B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元 花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同,销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系式yA=-x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系式yB=-x+14.
(1)求A、B两种型号的汽车的进货单价;
(2)已知A型汽车的售价比B型汽车的售价高2万元/台,设B型汽车售价为t万元/台.每周销售这两种车的总利润为W万元,求W与t的函数关系式,A、B两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?
(1)求A、B两种型号的汽车的进货单价;
(2)已知A型汽车的售价比B型汽车的售价高2万元/台,设B型汽车售价为t万元/台.每周销售这两种车的总利润为W万元,求W与t的函数关系式,A、B两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?
考点:二次函数的应用,分式方程的应用
专题:销售问题
分析:(1)利用花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相等,进而得出等式求出即可;
(2)分别表示出两种汽车的利润进而得出函数关系式求出最值即可.
(2)分别表示出两种汽车的利润进而得出函数关系式求出最值即可.
解答:解:(1)设A种型号的汽车的进货单价为m万元,
依题意得:
=
,
解得:m=10,
检验:m=10时,m≠0,m-2≠0,
故m=10是原分式方程的解,
故m-2=8.
答:A种型号的汽车的进货单价为10万元,B种型号的汽车的进货单价为8万元;
(2)根据题意得出:
W=(t+2-10)[-(t+2)+20]+(t-8)(-t+14)
=-2t2+48t-256,
=-2(t-12)2+32,
∵a=-2<0,抛物线开口向下,
∴当t=12时,W有最大值为32,
12+2=14,
答:A种型号的汽车售价为14万元/台,B种型号的汽车售价为12万元/台时,每周销售这两种车的总利润最大,最大总利润是32万元.
依题意得:
| 50 |
| m |
| 40 |
| m-2 |
解得:m=10,
检验:m=10时,m≠0,m-2≠0,
故m=10是原分式方程的解,
故m-2=8.
答:A种型号的汽车的进货单价为10万元,B种型号的汽车的进货单价为8万元;
(2)根据题意得出:
W=(t+2-10)[-(t+2)+20]+(t-8)(-t+14)
=-2t2+48t-256,
=-2(t-12)2+32,
∵a=-2<0,抛物线开口向下,
∴当t=12时,W有最大值为32,
12+2=14,
答:A种型号的汽车售价为14万元/台,B种型号的汽车售价为12万元/台时,每周销售这两种车的总利润最大,最大总利润是32万元.
点评:此题主要考查了二次函数的应用以及二次函数最值的求法,得出W与x的函数关系式是解题关键.

练习册系列答案
相关题目
若
是方程2x-ay=4的解,则a的值为( )
|
| A、1 | B、-1 | C、2 | D、-2 |
 如图,直线a∥b,c是截线.若∠2=4∠1,则∠1的度数为( )
如图,直线a∥b,c是截线.若∠2=4∠1,则∠1的度数为( )| A、30° | B、36° |
| C、40° | D、45° |
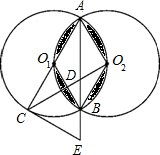 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.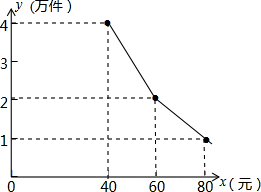 为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图.
为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图. 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴交于点A,与y轴交于点B,已知A(2,0),B(0,1),点C(-2,m)在直线AB上,反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴交于点A,与y轴交于点B,已知A(2,0),B(0,1),点C(-2,m)在直线AB上,反比例函数y=