题目内容
3.小夏是个数学谜,他不仅被书中的数学知识所吸引,而且爱探究为什么有这些数学知识,在这种“研究为什么”的精神支配下,他对数学思想中的“证明”饶有兴趣!最近,他证明了平行线间距离处处相等,并用这个定理证明了直角三角形中,两条直角边的平方和等于斜边的平方!(先以直角三角形的三边向外构造正方形,这样每边的平方可看作正方形的面积,最后用了平行线间距离处处相等定理得以解决.)请大家也来试一试
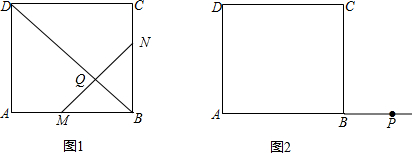
1)如图1,直线a∥b,A、B为a上任意两点,AC⊥b于C,BD⊥b于D,求证:AC=BD
2)如图2,△ABC中,∠BAC=90°,四边形ABED、ACGF、BCIH均为正方形(四边相等,四个角都是直角),AM⊥HI交BC于N,连结AH、CE
求证:①△EBC≌△ABH
②正方形ABED的面积=四边形BNMH的面积
③AB2+AC2=BC2.
分析 (1)先利用垂直于同一条直线的两直线平行,进而得出四边形ABDC是平行四边形,即可;
(2)①先判断出∠CBE=∠HBA,即可得出△EBC≌△ABH,得出结论;
②先判断出四边形BHMN是矩形,由全等三角形的面积相等即可得出结论;
③由②得出正方形ABED的面积=四边形BHMN面积,同理,正方形ACGF的面积=四边形CIMN的面积,最后用面积的合计可得出结论.
解答 证明:(1)∵AC⊥b于C,BD⊥b于D,
∴AC∥BD,
∵a∥b,
∴四边形ABDC是平行四边形,
∴AC=BD;
(2)①∵四边形ABED,BCIH是正方形,
∴AB=BE,BC=BH,∠ABE=∠CBH=90°,
∴∠ABC+∠ABE=∠ABC+∠CBH,∴∠CBE=∠HBA,
在△EBC和△ABH中,$\left\{\begin{array}{l}{BE=AB}\\{∠CBE=∠HBA}\\{BC=BH}\end{array}\right.$,
∴△EBC≌△ABH(SAS);
②∵四边形BCIH是正方形,
∴∠CBH=∠BHI=90°,
∵AM⊥HI,
∴∠AMH=90°=∠CBH=∠BHI=90°,
∴四边形BHMN是矩形,
由①知,△EBC≌△ABH,
∴S△EBC=S△ABH,
∵S△EBC=$\frac{1}{2}$BE•AB=$\frac{1}{2}$AB2,S△ABH=$\frac{1}{2}$BH•BN,
∴AB2=BH•BN,
∵S正方形ABED=AB2,S矩形BNMH=BH•BN,
∴S正方形ABED=S矩形BNMH,
即:正方形ABED的面积=四边形BNMH的面积;
(3)如图,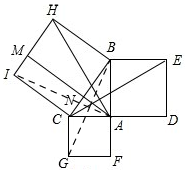
连接BG,AI,同②的方法,得出S正方形ACGF=S矩形CIMN,
∴S正方形ABED+S正方形ACGF=S矩形BHMN+S矩形CIMN=S正方形BCIH,
∵S正方形ABED=AB2,S正方形ACGF=AC2,S正方形BCIH=BC2,
∴AB2+AC2=BC2.
点评 此题是四边形综合题,主要考查了正方形的性质,全等三角形的判定和性质,三角形的面积公式,矩形的判定,矩形,正方形的面公式,解(1)的关键是判断出AC∥BD,解(2)①的关键是判断出∠CBE=∠HBA,解(2)②的关键是S△EBC=$\frac{1}{2}$BE•AB=$\frac{1}{2}$AB2,S△ABH=$\frac{1}{2}$BH•BN,解(2)③的关键是得出正方形的面积,是一道基础题目.

 53随堂测系列答案
53随堂测系列答案

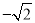 是2的平方根 B.
是2的平方根 B. 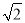 是2的平方根
是2的平方根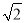 D. 2的算术平方根是
D. 2的算术平方根是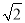
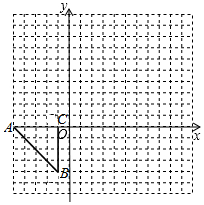 如图,直角坐标系中的△ABC的三个顶点分别为A(-5,0),B(-1,-4),C(-1,0).
如图,直角坐标系中的△ABC的三个顶点分别为A(-5,0),B(-1,-4),C(-1,0).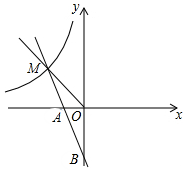 如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.
如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.