��Ŀ����
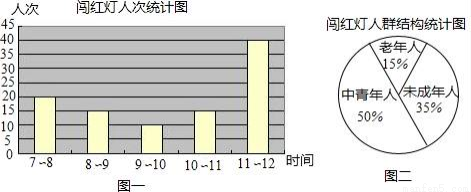
ijУ��ѧ����չ��������ƣ��䰮�������Ľ�����Ϊ��Уѧ����ίԱ��ij�쵽������ijʮ��·�ڣ��۲졢ͳ������7��00��12��00֮�䴳��Ƶ��˴Σ���������������ͳ��ͼ��
��1��ͼһ�и�ʱ�δ�����˴ε�ƽ����Ϊ�����˴Σ�
��2��ͼһ�и�ʱ�δ�����˴ε���λ���������˴Σ�
��3����·����һ������7��00��12��00֮�䴳��Ƶ�δ�������������˴Σ�
��4������һ�ܣ����죩�ڸ�·������7��00��12��00֮�䴳��Ƶ�������Լ�������˴Σ�
��5���Ƿ����Դ˹���ȫ����һ������7��00��12��00֮������·�ڴ���Ƶ��˴Σ�
��������Ϊʲô����������
��ϰ��ϵ�д�
�����Ŀ
18�� ��ͼ������������y=$\frac{k}{x}$��x��0����һ�κ���y=x+4��ͼ����A��B����ĺ�����ֱ�Ϊ-3��-1�������x�IJ���ʽ$\frac{k}{x}$��x+4��x��0���Ľ⼯Ϊ��������
��ͼ������������y=$\frac{k}{x}$��x��0����һ�κ���y=x+4��ͼ����A��B����ĺ�����ֱ�Ϊ-3��-1�������x�IJ���ʽ$\frac{k}{x}$��x+4��x��0���Ľ⼯Ϊ��������
 ��ͼ������������y=$\frac{k}{x}$��x��0����һ�κ���y=x+4��ͼ����A��B����ĺ�����ֱ�Ϊ-3��-1�������x�IJ���ʽ$\frac{k}{x}$��x+4��x��0���Ľ⼯Ϊ��������
��ͼ������������y=$\frac{k}{x}$��x��0����һ�κ���y=x+4��ͼ����A��B����ĺ�����ֱ�Ϊ-3��-1�������x�IJ���ʽ$\frac{k}{x}$��x+4��x��0���Ľ⼯Ϊ��������| A�� | x��-3 | B�� | -3��x��-1 | C�� | -1��x��0 | D�� | x��-3��-1��x��0 |
С�����ü���������һ��������������������������±���
���� | �� | 1 | 2 | 3 | 4 | 5 | �� |
��� | �� |
|
|
|
|
| �� |
��ô��������������8ʱ�������������( )��
A.  B.
B.  C.
C.  D.
D. 









 ��б���ϣ���б���ϵ�ƽ�澵����������ƽ�еĹ��ߣ�����������������ļнǦ���______�ȣ�
��б���ϣ���б���ϵ�ƽ�澵����������ƽ�еĹ��ߣ�����������������ļнǦ���______�ȣ�