Question

4．如图，点I为△ABC的内心，点O为△ABC的外心，若∠BIC=140°，则∠BOC=160°．

Answer 1

分析 因为点I为△ABC的内心，推出∠IAB+∠IBA=$\frac{1}{2}$（∠ABC+∠ACB）=180°-140°=40°，推出∠ABC+∠ACB=80°，推出∠A=180°-（∠ABC+∠ACB）=100°，
作△ABC的外接圆如图，在⊙O上取一点D，连接BD、CD．因为∠D=180°-∠A=80°，根据∠BOC=2∠D即可解决问题．

解答 解：∵点I为△ABC的内心，
∴∠IAB+∠IBA=$\frac{1}{2}$（∠ABC+∠ACB）=180°-140°=40°，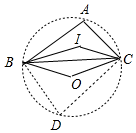
∴∠ABC+∠ACB=80°，
∴∠A=180°-（∠ABC+∠ACB）=100°
∵点O为△ABC的外心，作△ABC的外接圆如图，在⊙O上取一点D，连接BD、CD．
∴∠D=180°-∠A=80°，
∴∠BOC=2∠D=160°．
故答案为160．

点评 此题主要考查了三角形的内心和外心，正确把握三角形内心的性质是解题关键，记住钝角三角形的外心在三角形外，属于中考常考题型．