题目内容
1.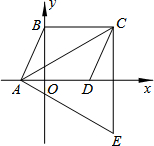 如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3$\sqrt{3}$),则D点的坐标为( )
如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3$\sqrt{3}$),则D点的坐标为( )| A. | (3,0) | B. | (4,0) | C. | (5,0) | D. | (6,0) |
分析 由题意得出AF垂直平分CE,AF平分∠CAE,由F的坐标得出OF、CF,根据三角函数求出AF,再证明Rt△CDF≌Rt△BAO,得出DF、OD,即可得出结果.
解答  解:如图所示:∵△ACE是等边三角形,点C与点E关于x轴对称,
解:如图所示:∵△ACE是等边三角形,点C与点E关于x轴对称,
∴AF垂直平分CE,AF平分∠CAE,
∴∠CFD=90°=∠BOA,CF=BO,
∵E点的坐标是(7,-3$\sqrt{3}$),
∴OF=7,CF=3$\sqrt{3}$,
在Rt△AFC中,∠CAF=30°,
∴AF=$\frac{CF}{tan30°}$=$\frac{3\sqrt{3}}{\frac{\sqrt{3}}{3}}$=9,
∴AO=AF-OF=2,
∵四边形ABCD为平行四边形,
∴AB=DC,
在Rt△CDF和Rt△BAO中,$\left\{\begin{array}{l}{DC=AB}\\{CF=BO}\end{array}\right.$,
∴Rt△CDF≌Rt△BAO(HL),
∴DF=AO=2,
∴OD=OF-DF=7-2=5,
∴D点坐标为(5,0);
故选:C.
点评 本题考查了平行四边形的性质、坐标与图形特征、等边三角形的性质、全等三角形的判定与性质、三角函数;熟练掌握平行四边形和等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.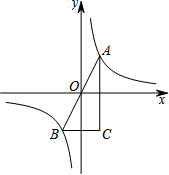 如图,A,B是函数y=$\frac{2}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,如果△ABC的面积记为S,那么( )
如图,A,B是函数y=$\frac{2}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,如果△ABC的面积记为S,那么( )
 如图,A,B是函数y=$\frac{2}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,如果△ABC的面积记为S,那么( )
如图,A,B是函数y=$\frac{2}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,如果△ABC的面积记为S,那么( )| A. | S=4 | B. | S=2 | C. | 2<S<4 | D. | S>4 |
10.下列调查方式合适的是( )
| A. | 对载人航天器“嫦娥二号”零部件的检查,采用抽样调查的方式 | |
| B. | 了解炮弹的杀伤力,采用全面调查的方式 | |
| C. | 对电视剧《来自星星的你》收视率的调查,采用全面调查的方式 | |
| D. | 对建阳市食品合格情况的调查,采用抽样调查的方式 |
 如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.
如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.
 四张形状相同的卡片如图所示.将卡片洗匀后背面朝上放置在桌面上,小明先随机抽一张卡片,记下数字为x;小亮再随机抽一张卡片,记下数字为y.两人在此基础上共同协商一个游戏规则:当x>y时小明获胜,否则小亮获胜
四张形状相同的卡片如图所示.将卡片洗匀后背面朝上放置在桌面上,小明先随机抽一张卡片,记下数字为x;小亮再随机抽一张卡片,记下数字为y.两人在此基础上共同协商一个游戏规则:当x>y时小明获胜,否则小亮获胜