题目内容
6.列方程解应用题我国元朝朱世杰所著的《算学启蒙》(1299年)一书,有一道题目是:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”
译文是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?
分析 设快马x天可以追上慢马,根据慢马先行的路程=快慢马速度之差×快马行走天数,即可列出关于x的一元一次方程,解之即可得出结论.
解答 解:设快马x天可以追上慢马,
由题意,得240x-150x=150×12,
解得:x=20.
答:快马20天可以追上慢马.
点评 本题考查了一元一次方程的应用,根据数量关系列出关于x的一元一次方程是解题的关键.

练习册系列答案
相关题目
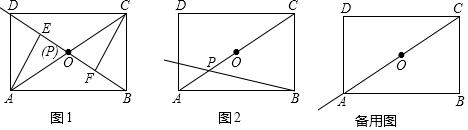
16. 如图,正方形ABCD的边长为1,电子蚂蚁P从点A分别以1个单位/秒的速度顺时针绕正方形运动,电子蚂蚁Q从点A以3个单位/秒的速度逆时针绕正方形运动,则第2017次相遇在( )
如图,正方形ABCD的边长为1,电子蚂蚁P从点A分别以1个单位/秒的速度顺时针绕正方形运动,电子蚂蚁Q从点A以3个单位/秒的速度逆时针绕正方形运动,则第2017次相遇在( )
 如图,正方形ABCD的边长为1,电子蚂蚁P从点A分别以1个单位/秒的速度顺时针绕正方形运动,电子蚂蚁Q从点A以3个单位/秒的速度逆时针绕正方形运动,则第2017次相遇在( )
如图,正方形ABCD的边长为1,电子蚂蚁P从点A分别以1个单位/秒的速度顺时针绕正方形运动,电子蚂蚁Q从点A以3个单位/秒的速度逆时针绕正方形运动,则第2017次相遇在( )| A. | 点 A | B. | 点B | C. | 点C | D. | 点D |
11.某项工程甲单独做4天完成,乙单独做6天完成,若甲先做1天,然后甲、乙合作完成此项工程,若设甲一共做了x天,则所列方程为( )
| A. | $\frac{x}{4}$+$\frac{x+1}{6}$=1 | B. | $\frac{x}{4}$+$\frac{x-1}{6}$=1 | C. | $\frac{x+1}{4}$+$\frac{x}{6}$=1 | D. | $\frac{x}{4}$+$\frac{1}{4}$+$\frac{x-1}{6}$=1 |
16.下列图形中,是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=120°,射线OC的方向是北偏东80°.
如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=120°,射线OC的方向是北偏东80°.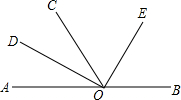 如图,O为直线AB上一点,∠AOC=46°,OD平分∠AOC,∠DOE=90°,
如图,O为直线AB上一点,∠AOC=46°,OD平分∠AOC,∠DOE=90°,