题目内容
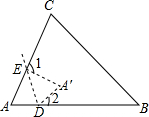 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE重叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE重叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )| A、120° | B、110° |
| C、100° | D、80° |
考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:先根据图形翻折变化的性质得出△ADE≌△A′DE,∠AED=∠A′ED,∠ADE=∠A′DE,再根据三角形内角和定理求出∠AED+∠ADE及∠A′ED+∠A′DE的度数,然后根据平角的性质即可求出答案.
解答:解:∵△A′DE是△ABC翻折变换而成,
∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=60°,
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-60°=120°,
∴∠1+∠2=360°-2×120°=120°.
故选A.
∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=60°,
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-60°=120°,
∴∠1+∠2=360°-2×120°=120°.
故选A.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
当x>0,y<0时,则x,x+y,x-y中最大的数是( )
| A、x | B、x+y |
| C、x-y | D、以上答案不对 |
实数a、b在数轴上的位置如图所示,那么化简|b-a|-
的结果是( )

| a2 |

| A、2a-b | B、b |
| C、-b | D、-2a+b |
已知两个相似多边形的相似比是3:4,其中较小多边形的周长为36cm,则较大多边形的周长为( )
| A、48cm | B、54cm |
| C、56cm | D、64cm |
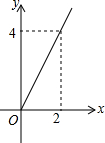 王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为
王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为
 已知:如图△ABC.
已知:如图△ABC.