题目内容
已知1+x+x2+x3+x4=0，求1+x+x2+x3+…+x2015的值．
考点：因式分解的应用
专题：计算题
分析：原式五项五项结合，提取公因式后，将已知等式代入计算即可求出值．
解答：解：∵1+x+x2+x3+x4=0，
∴1+x+x2+x3+…+x2015=（1+x+x2+x3+x4）+x5（1+x+x2+x3+x4）+…+x2011（1+x+x2+x3+x4）=0．
∴1+x+x2+x3+…+x2015=（1+x+x2+x3+x4）+x5（1+x+x2+x3+x4）+…+x2011（1+x+x2+x3+x4）=0．
点评：此题考查了因式分解的应用，熟练掌握运算法则是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
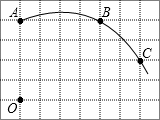如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
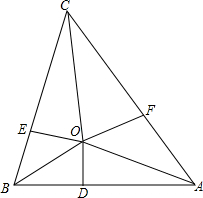如图，已知在△ABC中，AO、BO、CO分别是∠BAC、∠ABC、∠ACB的角平分线，AB=4，BC=5，CA=6，OD⊥AB，OE⊥BC，OF⊥AC，求OD的长．