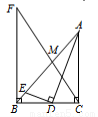
题目内容
(本题满分10分)如图1,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D是BC上一定点.动点P从C出发,以2cm/s的速度沿C→A→B方向运动,动点Q从D出发,以1cm/s的速度沿D→B方向运动.点P出发5 s后,点Q才开始出发,且当一个点达到B时,另一个点随之停止.图2是当 时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.
时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.

(1)CD = ,  ;
;
(2)当点P在边AB上时,t为何值时,使得△BPQ与△ABC为相似?
(3)运动过程中,求出当△BPQ是以BP为腰的等腰三角形时t的值.
(1)CD=2,a=10.8;(2)4.25秒或6秒;(3)5秒或 秒
秒
【解析】
试题分析:(1)当点P运动到点A时,△BPQ的面积为18,
∴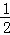 •6•BD=18,解得BD=6,
•6•BD=18,解得BD=6,
∴CD=BC﹣BD=2,
当t=5s时,AP=2×5﹣6=4,点Q在D点,点P在AB上如图①,作PH⊥BC于H,
在Rt△ABC中,AC=6,BC=8,
∴AB=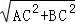 =10,
=10,
∵PH∥AC,
∴△BPH∽△BAC,
∴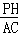 =
=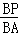 ,即
,即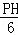 =
=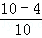 ,解得PH=
,解得PH=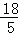 ,
,
∴S△PBQ=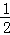 ×6×
×6×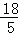 =
=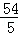 ,
,
即a=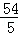 ;
;
故答案为:2,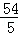 ;
;
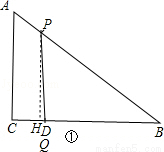
(2)点P在边AB上,
当3<t≤5,点Q在D点,BP=16﹣2t,
若PD⊥BC,△BPQ∽△BAC,
∴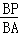 =
=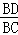 ,即
,即 =
=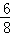 ,解得t=
,解得t= ;
;
当5<t≤8,DQ=t﹣5,则BQ=8﹣2﹣(t﹣5)=11﹣t,BP=16﹣2t,
当∠PQB=90°时,△BPQ∽△BAC,如图②,
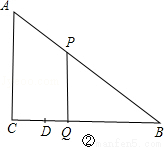
∵△BPQ∽△BAC,
∴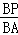 =
=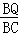 ,即
,即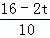 =
=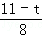 ,解得t=3,不合题意舍去;
,解得t=3,不合题意舍去;
当∠BPQ=90°时,△BPQ∽△BAC,如图③,
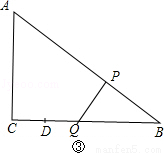
∵△BPQ∽△BCA,
∴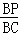 =
=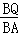 ,即
,即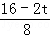 =
=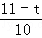 ,解得t=6,
,解得t=6,
综上所述,当t为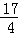 或6时,△BPQ与△ABC为相似;
或6时,△BPQ与△ABC为相似;
(3)PB=16﹣2t,BQ=11﹣t,
当BP=BQ,则16﹣2t=11﹣t,解得t=5;
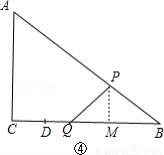
当PB=PQ,作PM⊥BC于M,如图④,则BM= BQ=
BQ= (11﹣t),
(11﹣t),
∵PM∥AC,
∴△BPM∽△BAC,
∴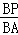 =
= ,即
,即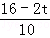 =
=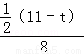 ,解得t=
,解得t=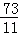 ,
,
综上所述,当△BPQ是以BP为腰的等腰三角形时t的值为5或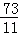 .
.
考点:1.相似形综合题;2.动点问题的函数图象;3.勾股定理的应用

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案




 ;③AC·BE=12;④3BF=4AC.其中正确结论的个数有( )
;③AC·BE=12;④3BF=4AC.其中正确结论的个数有( )