Question

一张纸上有一个圆．

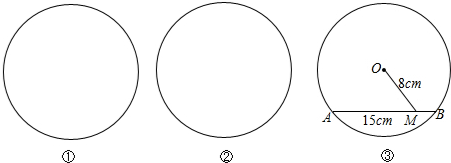
（1）如图①，请用尺规作图，作出圆的圆心（保留作图痕迹，不写作法和证明）；
（2）如图②，若不用尺规作图，你还有其它作法吗？请说明作法（不作图）；
（3）如图③，⊙O表示一个圆形工件，图中标注了有关尺寸，并且MB：MA=1：4，求工件半径的长．

Answer 1

考点：圆的综合题

专题：

分析：（1）作出弦的垂直平分线，再结合垂径定理推论得出圆心位置；
（2）利用圆周角定理推论得出直径位置，两直径交点即为圆心的位置；
（3）利用勾股定理以及垂径定理得出EO的平方以及AE的值，进而得出AO的长．

解答：解：（1）如图①所示，在圆中作任意2条弦的垂直平分线，由垂径定理可知这2条垂直平分线必定与圆的2条直径重合，所以交点O即为所求；

（2）如图②所示，90°的圆周角所对的弦是直径，则利用直角三角板作出圆的两条直径，交点O即为所求；

（3）如图③所示，连接AO，过点O作OE⊥AB于点E，

∵MB：MA=1：4，AB=15cm，
∴BM=3cm，AM=12cm，AE=BE=

15

2

cm，
∴EM=12-

15

2

=

9

2

cm，
∴OE²=8²-(

9

2

)2=

175

4

，
∴AO=

AE2+OE2

=

( 15 2 )2+ 175 4

=10cm，
答：工件半径的长为10cm．

点评：此题主要考查了圆的综合应用、垂径定理和圆周角定理等知识，熟练利用勾股定理得出AO的长是解题关键．