题目内容
4.(1)如图,AD∥BC,∠A=∠DEC=90°,DE=EC,试说明AD+BC=AB.(2)在△ABC和△DCE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,CF⊥AD,试说明GB=EG.
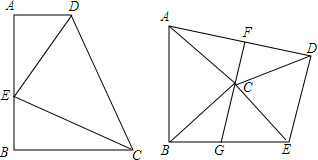
分析 (1)推出∠ADE=∠BEC,根据AAS证△AED≌△CEB,推出AE=BC,BE=AD,即可得出结论.
(2)作BM⊥FG于M,EN⊥FG于N,则BM∥EN,由AAS证明△BCM≌△CAF,得出对应边相等BM=CF,同理:△CEN≌△DCF,得出EN=CF,因此BM=EN,由平行线得出比例式GB:GE=BM:EN=1,即可得出结论.
解答 (1)证明:∵∠DEC=∠A=90°,
∴∠ADE+∠AED=90°,∠AED+∠BEC=90°,
∴∠ADE=∠BEC,
∵AD∥BC,∠A=90°,
∴∠B+∠A=180°,
∴∠B=∠A=90°,
在△AED和△CEB中,$\left\{\begin{array}{l}{∠A=∠B}&{\;}\\{∠ADE=∠BEC}&{\;}\\{DE=EC}&{\;}\end{array}\right.$,
∴△AED≌△CEB,
∴AE=BC,BE=AD,
∵AE+BE=AB,
∴AD+BC=AB.
(2)证明:作BM⊥FG于M,EN⊥FG于N,如图所示:
则BM∥EN,
∵∠ACB=90°,CF⊥AD,
∴∠AFC=90°,∠BCM+∠ACF=90°,∠ACF+∠CAF=90°,
∴∠BCM=∠CAF,
在△BCM和△CAF中,$\left\{\begin{array}{l}{∠BCM=∠CAF}&{\;}\\{∠BMC=∠AFC=90°}&{\;}\\{BC=CA}&{\;}\end{array}\right.$,
∴△BCM≌△CAF(AAS),
∴BM=CF,
同理:△CEN≌△DCF,
∴EN=CF,
∴BM=EN,
∵BM∥EN,
∴GB:GE=BM:EN=1,
∴GB=EG.
点评 本题考查了等腰直角三角形的性质、全等三角形的性质和判定、平行线的性质、平行线分线段成比例定理等知识;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| 类别 | A | B |
| 成本(万元/套) | 30 | 40 |
| 售价(万元/套) | 35 | 47 |
(2)由于市场变化,公司将每套A型设备的售价提高a万元(a>0),每套B型设备的售价保持不变,若所制造的这两种设备可全部售出,则哪种方案能获得最大利润?(注:利润=售价-成本)
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,我校一块边长为2x米的正方形空地是八年级1-4班的卫生区,学校把它分成大小不同的四块,采用抽签的方式安排卫生区,下图是四个班级所抽到的卫生区情况,其中1班的卫生区是一块边长为(x-2y)米的正方形,其中0<2y<x.
如图,我校一块边长为2x米的正方形空地是八年级1-4班的卫生区,学校把它分成大小不同的四块,采用抽签的方式安排卫生区,下图是四个班级所抽到的卫生区情况,其中1班的卫生区是一块边长为(x-2y)米的正方形,其中0<2y<x.