题目内容
20.已知函数y=$\left\{\begin{array}{l}{{-(x-1)}^{2}+1(x≤3)}\\{{-(x-5)}^{2}+1(x>3)}\end{array}\right.$(1)若使y=k成立的x的值恰好有三个,则k=-3;
(2)若使y=k成立的x的值恰好有两个,则k的取值范围为k=1或k<-3.
分析 首先在坐标系中画出已知函数y=$\left\{\begin{array}{l}{{-(x-1)}^{2}+1(x≤3)}\\{{-(x-5)}^{2}+1(x>3)}\end{array}\right.$的图象,
(1)利用数形结合的方法即可找到使y=k成立的x值恰好有三个的k值.
(2)利用数形结合的方法即可找到使y=k成立的x值恰好有两个的k值.
解答 解:函数y=$\left\{\begin{array}{l}{{-(x-1)}^{2}+1(x≤3)}\\{{-(x-5)}^{2}+1(x>3)}\end{array}\right.$的图象如图:
(1)根据图象知道当y=-3时,对应成立的x有恰好有三个,
∴k=-3.
(2)根据图象知道当y=1或y<-3时,对应成立的x有恰好有2个,
所以k=1或k<-3.
故答案为:-3;k=1或k<-3.
点评 此题主要考查了利用二次函数的图象解决交点问题,解题的关键是把解方程的问题转换为根据函数图象找交点的问题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
1.长春市2014年城市道路改建总投资达到209亿元,用科学记数法表示209亿元应为( )
| A. | 209×108元 | B. | 209×109元 | C. | 2.09×1010元 | D. | 2.09×1011元 |
2. 如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )
如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )
 如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )
如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )| A. | 10 | B. | 8 | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{3}$ |
 已知:在△ABC中,∠A=60°,∠B=45°,AB=2.求△ABC的面积(结果可保留根号).
已知:在△ABC中,∠A=60°,∠B=45°,AB=2.求△ABC的面积(结果可保留根号).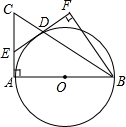 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,BF⊥DE于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,BF⊥DE于点F.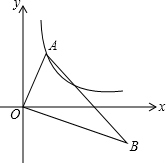 如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6.
如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6. 如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8.
如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8. 已知平行四边形ABCD中,AB=BD=CD,且DB⊥AB,求tan∠CAB、tan∠DAC的值.
已知平行四边形ABCD中,AB=BD=CD,且DB⊥AB,求tan∠CAB、tan∠DAC的值.