题目内容
6. 如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF.
如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF.(1)判断△CDF的形状并证明.
(2)若BC=6,AF=2,求AB的长.
分析 (1)理由“ASA”证明△ADF≌△BCD得到DF=CD,∠ADF=∠BCD,再利用∠BCD+∠CDB=90°得到∠CDF=90°,则可判断△CDF为等腰直角三角形;
(2)由△ADF≌△BCD得到AD=BC=6,AF=BD=2,然后计算AD-BD即可.
解答 解:(1)△CDF为等腰直角三角形.理由如下:
∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中
$\left\{\begin{array}{l}{AF=DB}\\{∠DAF=∠CBD}\\{AB=BC}\end{array}\right.$,
∴△ADF≌△BCD,
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴△CDF为等腰直角三角形;
(2)∵△ADF≌△BCD,
∴AD=BC=6,AF=BD=2,
∴AB=AD-BD=6-2=4.
点评 本题考查了全等三角形的判定与性质全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
15. 如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )
如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )
 如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )
如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )| A. | 2α+∠A=180° | B. | α+∠A=90° | C. | 2α+∠A=90° | D. | α+∠A=180° |
 如图.在平面直角坐标系中,点O为坐标原点,抛物线y=$\frac{5}{18}$x2+bx+c与x轴的交点分别为点A、B,与y轴的交点为点C,直线BC的解析式为y=$\frac{1}{3}$x-3.
如图.在平面直角坐标系中,点O为坐标原点,抛物线y=$\frac{5}{18}$x2+bx+c与x轴的交点分别为点A、B,与y轴的交点为点C,直线BC的解析式为y=$\frac{1}{3}$x-3. 如图,在△ABC中,∠C=90°,DE垂直平分AB,E是垂足,交BC于D,DG⊥AD于D,且DG=BD,AC=8,CD=6,求△BDG的面积.
如图,在△ABC中,∠C=90°,DE垂直平分AB,E是垂足,交BC于D,DG⊥AD于D,且DG=BD,AC=8,CD=6,求△BDG的面积.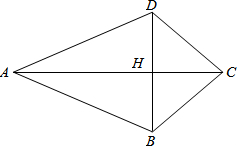 如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.
如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.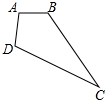 如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.