Question

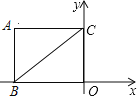
【题目】通过学习锐角三角比，我们知道在直角三角形中，一个锐角的大小与两条边长的比值是一一对应的，因此，两条边长的比值与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做底角的邻对（can），如图（1）在△ABC中，AB＝AC，底角B的邻对记作canB，这时canB＝底边/腰=，容易知道一个角的大小与这个角的邻对值也是一一对应的．根据上述角的邻对的定义，解下列问题：

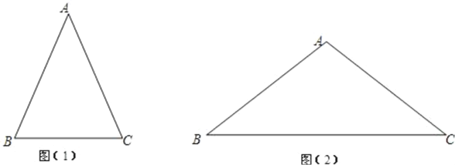
（1）can30°＝　 　；

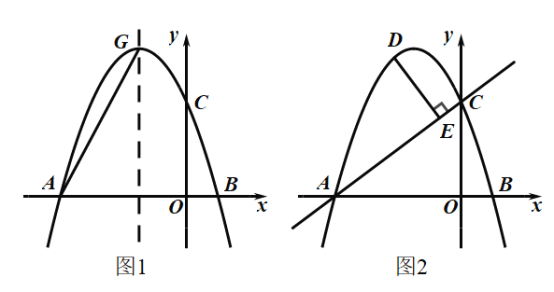
（2）如图（2），已知在△ABC中，AB＝AC，canB＝，S△ABC＝24，求△ABC的周长．

Answer 1

【答案】（1）；（2）18

【解析】

（1）过点A作AD⊥BC于点D，根据∠B=30°，可得出BD=AB，结合等腰三角形的性质可得出BC=AB，继而得出canB；

（2）过点A作AE⊥BC于点E，根据canB=，设BC=8x，AB=5x，再由S△ABC=24，可得出x的值，继而求出周长．

解：（1）过点A作AD⊥BC于点D，

∵∠B＝30°，

∴cos∠B＝＝，

∴BD＝AB，

∵△ABC是等腰三角形，

∴BC＝2BD＝AB，

∴can30°＝＝；

故答案为：；

（2）过点A作AE⊥BC于点E，

∵canB＝，则可设BC＝8x，AB＝5x，

∴AE＝＝3x，

∵S△ABC＝24，

∴BC×AE＝12x2＝24，

解得：x＝，

∴AB＝AC＝5，BC＝8，

∴可得△ABC的周长为18．