题目内容
11.解不等式组$\left\{\begin{array}{l}{x+4≥2①}\\{2x+6≥3x+3②}\end{array}\right.$请结合题意填空,完成本题的解答:
(Ⅰ)解不等式①,得x≥-2;
(Ⅱ)解不等式②,得x≤3;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
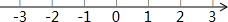
(Ⅳ)原不等式组的解集为-2≤x≤3.
分析 (I)移项,合并同类项,系数化成1即可;
(II)移项,合并同类项,系数化成1即可;
(III)在数轴上表示出来即可;
(IV)根据数轴得出即可.
解答 解:(I)x+4≥2
x≥2-4
x≥-2,
故答案为:x≥-2;
(II)2x+6≥3x+3,
2x-3x≥3-6,
-x≥-3,
x≤3,
故答案为:x≤3;
(III)在数轴上表示为: ;
;
(IV)原不等式组的解集为-2≤x≤3,
故答案为:-2≤x≤3.
点评 本题考查了解一元一次不等式,解一元一次不等式组,在数轴上表示不等式的解集的应用,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.等腰△ABC的周长为10,则其腰长x的取值范围是( )
| A. | x>$\frac{5}{2}$ | B. | x<5 | C. | $\frac{5}{2}$<x<5 | D. | $\frac{5}{2}$≤x≤5 |
6.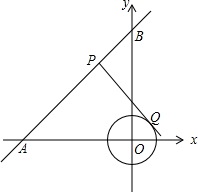 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{119}}{5}$ | C. | 2.4 | D. | 3 |
1.如图,有5张扑克牌,从中随机抽取一张,点数是2的倍数的概率为( )


| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
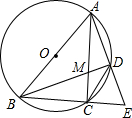 如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.
如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M. 如图,M为正方形ABCD边AB上一点,DN⊥DM交BC的延长线于点N.求证:AM=CN.
如图,M为正方形ABCD边AB上一点,DN⊥DM交BC的延长线于点N.求证:AM=CN.