题目内容
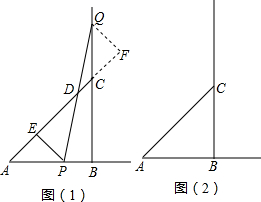 (1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,过P作PE⊥AC于点E.设P点运动时间为t.
(1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,过P作PE⊥AC于点E.设P点运动时间为t.①当点P在线段AB上运动时,线段DE的长度是否改变?若不改变,求出DE的值;若改变,请说明理由.
下面给出一种解题的思路,你可以按这一思路解题,也可以选择另外的方法解题.
解:过Q作QF⊥直线AC于点M
∵PE⊥AC于点E,QF⊥直线AC于点M
∴∠AEP=∠F=90°
(下面请你完成余下的解题过程)
②当点P在线段AB的延长线上运动时,(1)中的结论是否还成立?请在图2画出图形并说明理由.
(2)若将(1)中的“腰长为10cm的等腰直角△ABC”改为“边长为a的等边△ABC”时(其余条件不变),则线段DE的长度又如何?(直接写出答案,不需要解题过程)
(3)若将(2)中的“等边△ABC”改为“△ABC”(其余条件不变),请你做出猜想:当△ABC满足
∠A=∠ACB
∠A=∠ACB
条件时,(2)中的结论仍然成立.(直接写出答案,不需要解题过程)分析:(1)①求出AC的值,过Q作QF⊥AC交AC的延长线于F,根据AP=CQ=t和等腰直角三角形求出AE=PE=QF=CF,根据平行线分线段成比例定理求出DE=DF,即可求出答案;②根据AAS证△APE和△CFQ全等,推出CF=AE,推出AC=EF即可;
(2)与①证法类似求出DE=DF,AE=CF=
EF,推出EF=AC,代入求出即可;
(3)根据①的结论求出只要∠A=∠ACB时,就能推出AE=CF,即可求出答案.
(2)与①证法类似求出DE=DF,AE=CF=
| 1 |
| 2 |
(3)根据①的结论求出只要∠A=∠ACB时,就能推出AE=CF,即可求出答案.
解答: 解:(1)①线段DE的长度不变,
解:(1)①线段DE的长度不变,
由勾股定理得:AC=
=10
,
过Q作QF⊥AC交AC的延长线于F,
∵∠QCF=∠ACB=∠A=∠EPA=45°,AP=CQ=t,
∴AE=PE=QF=CF,
∵QF⊥AC,PE⊥AC,
∴QF∥PE,
∴
=
,
∴DE=DF=
EF=
(EC+CF)=
(EC+AE)=
AC=5
.
②成立,
理由是:在△AEP和△CFQ中
,
∴△AEP≌△CFQ,
∴AE=CF,
∴AC=AE+CE=CF+CE=EF,
由①知:DE=DF=
EF,
∴DE=
AC,
∴成立.
(2)与①证法类似:知DE=DF,EF=AC,
∴DE=
a.
(3)当∠A=∠ACB时,
∵∠DCF=∠ACB=∠A,
在△AEP和△CFQ中
,
∴△AEP≌△CFQ,
∴AE=CF,
∴AE+EC=CF+EC,
即AC=EF,
由①知ED=DF,
∴DE=
AC,
∴故答案为:∠A=∠ACB.
 解:(1)①线段DE的长度不变,
解:(1)①线段DE的长度不变,由勾股定理得:AC=
| AB2+BC2 |
| 2 |
过Q作QF⊥AC交AC的延长线于F,
∵∠QCF=∠ACB=∠A=∠EPA=45°,AP=CQ=t,
∴AE=PE=QF=CF,
∵QF⊥AC,PE⊥AC,
∴QF∥PE,
∴
| PE |
| QF |
| ED |
| DF |
∴DE=DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
②成立,
理由是:在△AEP和△CFQ中
|
∴△AEP≌△CFQ,
∴AE=CF,
∴AC=AE+CE=CF+CE=EF,
由①知:DE=DF=
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
∴成立.

(2)与①证法类似:知DE=DF,EF=AC,
∴DE=
| 1 |
| 2 |
(3)当∠A=∠ACB时,
∵∠DCF=∠ACB=∠A,

在△AEP和△CFQ中
|
∴△AEP≌△CFQ,
∴AE=CF,
∴AE+EC=CF+EC,
即AC=EF,
由①知ED=DF,
∴DE=
| 1 |
| 2 |
∴故答案为:∠A=∠ACB.
点评:本题考查了等边三角形性质,等腰三角形的性质,勾股定理,全等三角形的性质和判定,平行线分线段成比例定理等知识点的运用,主要考查学生运用性质进行推理,能根据证明过程得出证题规律和结果规律是解此题的关键,只要掌握证①的规律,此题就能迎刃而解.

练习册系列答案
相关题目
 如图,等腰△ABC的周长32cm,底边长12cm.则高AD=
如图,等腰△ABC的周长32cm,底边长12cm.则高AD= 如图,已知等腰△ABC的周长是16,底边BC上的高AD的长是4,求这个三角形各边的长.
如图,已知等腰△ABC的周长是16,底边BC上的高AD的长是4,求这个三角形各边的长.