题目内容
写出一个经过点(2,5)且y随x的增大而减小的一次函数关系式 (写出一个即可).
考点:一次函数的性质
专题:开放型
分析:由一次函数过(2,5),设出一次函数解析式为y=kx+b,将此点代入得到2k+b=5,又此一次函数y随x的增大而减小,可得出k小于0,取k=-2,可得出b=9,确定出满足题意的一次函数解析式.
解答:解:设一次函数的解析式为y=kx+b(k≠0),
将x=2,y=5代入得:2k+b=5,
又此一次函数y随x的增大而减小,
∴k<0,
若k=-2,可得出b=9,
则一次函数为y=-2x+9.
故答案为:y=-2x+9.
将x=2,y=5代入得:2k+b=5,
又此一次函数y随x的增大而减小,
∴k<0,
若k=-2,可得出b=9,
则一次函数为y=-2x+9.
故答案为:y=-2x+9.
点评:此题考查了一次函数的性质,一次函数y=kx+b(k≠0),当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.此外本题的答案不唯一,只要满足k为负数,且k+b=1即可.

练习册系列答案
相关题目
已知:下列命题中,
(1)三点确定一个圆;
(2)内错角相等;
(3)已知反比例函数y=-
,若x>1,则y>-2;
(4)对角线互相垂直平分且相等的四边形是正方形;
其中真命题的个数有( )
(1)三点确定一个圆;
(2)内错角相等;
(3)已知反比例函数y=-
| 2 |
| x |
(4)对角线互相垂直平分且相等的四边形是正方形;
其中真命题的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若二次三项式x2+mx+9是完全平方式,则m的值等于( )
| A、3 | B、3或-3 |
| C、6 | D、6或-6 |
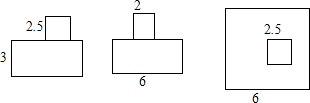 已知一个模型的三视图如图所示,(单位:m)
已知一个模型的三视图如图所示,(单位:m)