题目内容
8.△ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为BC、CA、AB上的点,则△EFG周长的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
分析 在BC上任取一点E,连接AE,把△ABE沿AB翻折得△ABE′,把△ACE沿AC翻折得△ACE″,由∠BAC=60°,推出∠E′AE″=120°,AE=AE′=AE″,连接E′E″交AB、AC于G、F.连接GE,EF,由GE=E′G,EF=E″F,因为△GEF的周长=GE+GF+EF=E′G+GF+E″F=E′E″=$\sqrt{3}$AE,根据垂线段最短可知AD⊥BC时AD的值最小,所以当点E与点D重合时,AE最小,
解答 解:在BC上任取一点E,连接AE,
把△ABE沿AB翻折得△ABE′,把△ACE沿AC翻折得△ACE″,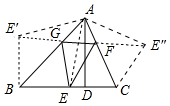
∵∠BAC=60°,
∴∠E′AE″=120°,AE=AE′=AE″,
连接E′E″交AB、AC于G、F.连接GE,EF,
∵GE=E′G,EF=E″F,
∴△GEF的周长=GE+GF+EF=E′G+GF+E″F=E′E″=$\sqrt{3}$AE,
∵根据垂线段最短可知AD⊥BC时AD的值最小,
∴当点E与点D重合时,AE最小,
∴△DEF的周长的最小值=$\sqrt{3}$×$\sqrt{3}$=3.
故选C.
点评 本题考查了轴对称的性质,等腰三角形的性质,最短路线问题,解题的关键是学会利用垂线段最短解决最短问题,作出G、E、F点是本题的关键.

练习册系列答案
相关题目
18.方程x2+2x+3=0的两根的情况是( )
| A. | 有两个不相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个相同的实数根 | D. | 不能确定 |
19.下列图形中具有稳定性的是( )
| A. | 平行四边形 | B. | 等腰三角形 | C. | 长方形 | D. | 梯形 |
16.据瑞安市统计局统计,2015年瑞安市国民生产总值达720亿元,数据720亿用科学记数法可表示为( )
| A. | 7.20×102 | B. | 7.20×1010 | C. | 0.720×1011 | D. | 720×108 |
6.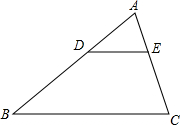 如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )
如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )
 如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )
如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 3:2 |
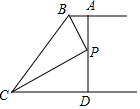 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )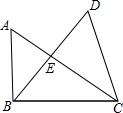 图中有几个三角形?用符号表示这些三角形.
图中有几个三角形?用符号表示这些三角形.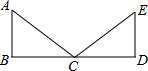 如图,已知 AB⊥BD,ED⊥BD,AB=ED,要说明△ABC≌△EDC,
如图,已知 AB⊥BD,ED⊥BD,AB=ED,要说明△ABC≌△EDC,