��Ŀ����
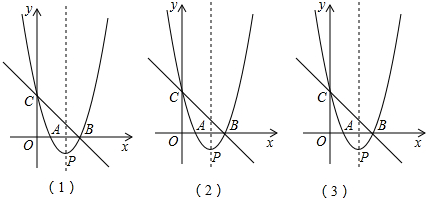
��ͼ��1����ֱ��y=-x+3��x�ᡢy��ֱ��ڵ�B����C������B��C�����������y=x2+bx+c��x�����һ������ΪA������ΪP��
��1����������ߵĽ���ʽ��
��2����0��x��3ʱ��������������һ��E��ʹ��CBE����������ֵ��
��3������AC����x�����Ƿ���ڵ�Q��ʹ��P��B��QΪ��������������ABC���ƣ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
��4���ڸ������ߵĶԳ������Ƿ���ڵ�M��ʹ��C��P��MΪ�����������Ϊ���������Σ������ڣ���������з��������ĵ�M�����ꣻ�������ڣ���˵�����ɣ���ͼ��2����ͼ��3������ͼ̽����
��1����������ߵĽ���ʽ��
��2����0��x��3ʱ��������������һ��E��ʹ��CBE����������ֵ��
��3������AC����x�����Ƿ���ڵ�Q��ʹ��P��B��QΪ��������������ABC���ƣ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
��4���ڸ������ߵĶԳ������Ƿ���ڵ�M��ʹ��C��P��MΪ�����������Ϊ���������Σ������ڣ���������з��������ĵ�M�����ꣻ�������ڣ���˵�����ɣ���ͼ��2����ͼ��3������ͼ̽����

���㣺���κ����ۺ���
ר�⣺
��������1��ֱ�����ô���ϵ��������κ�������ʽ���ɣ�
��2������E��x��Ĵ���FE�����ȱ�ʾ��E��F�����꣬�����ó�S��CBE=S��CEF+S��BEF�������ö��κ�����ֵ�ó��𰸣�
��3�����õ�
=
ʱ����
=
ʱ���ֱ����Q�����ꣻ
��4���ֱ����õ�CM1=PC����PC=PM2����CM3=PM3����PC=PM4���������������������꼴�ɣ�
��2������E��x��Ĵ���FE�����ȱ�ʾ��E��F�����꣬�����ó�S��CBE=S��CEF+S��BEF�������ö��κ�����ֵ�ó��𰸣�
��3�����õ�
| BQ |
| BP |
| BC |
| BA |
| BQ |
| BP |
| BA |
| BC |
��4���ֱ����õ�CM1=PC����PC=PM2����CM3=PM3����PC=PM4���������������������꼴�ɣ�
����⣺��1������֪����B��3��0����C��0��3����
��
��
���
��
�������߽���ʽΪy=x2-4x+3��
��2����ͼ��1����0��x��3ʱ���ڴ�����������ȡһ��E������CE��BE��������E��x��Ĵ���FE����ֱ��BC�ڵ�F��
���F��x��-x+3������E��x��x2-4x+3����
��EF=-x2+3x��
��S��CBE=S��CEF+S��BEF=
EF•OB=-
x2+
x=-(x-
)2+
��
��a=-
��0��
�൱x=
ʱ��S��CBE�����ֵ��
��y=x2-4x+3=-
��
��E��
��-
����
��3����ͼ��2����
�ɣ�1������A��1��0��������BP��
�ߡ�CBA=��ABP=45�㣬
�൱
=
ʱ����ABC�ס�PBQ��
��BQ=3����Q1��0��0����
�൱
=
ʱ����ABC�ס�QBP��
��BQ=
����Q2��
��0����

��4����ͼ��3��������PC��
��y=x2-4x+3=��x-2��2-1����Գ���Ϊx=2����������ΪP��2��-1����
��PC=2
����CM1=PC����M1��2��7����
��PC=PM2����M2��2��2
-1����
��CM3=PM3����M3��2��
����
��PC=PM4����M4��2��-2
-1����
�����������ĵ�M�ֱ�ΪM1��2��7����M2��2��2
-1����
M3��2��
����M4��2��-2
-1����
��
|
���
|
�������߽���ʽΪy=x2-4x+3��
��2����ͼ��1����0��x��3ʱ���ڴ�����������ȡһ��E������CE��BE��������E��x��Ĵ���FE����ֱ��BC�ڵ�F��
���F��x��-x+3������E��x��x2-4x+3����
��EF=-x2+3x��
��S��CBE=S��CEF+S��BEF=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
��a=-
| 3 |
| 2 |
�൱x=
| 3 |
| 2 |
��y=x2-4x+3=-
| 3 |
| 4 |
��E��
| 3 |
| 2 |
| 3 |
| 4 |
��3����ͼ��2����
�ɣ�1������A��1��0��������BP��
�ߡ�CBA=��ABP=45�㣬
�൱
| BQ |
| BP |
| BC |
| BA |
��BQ=3����Q1��0��0����
�൱
| BQ |
| BP |
| BA |
| BC |
��BQ=
| 2 |
| 3 |
| 7 |
| 3 |

��4����ͼ��3��������PC��
��y=x2-4x+3=��x-2��2-1����Գ���Ϊx=2����������ΪP��2��-1����
��PC=2
| 5 |
��PC=PM2����M2��2��2
| 5 |
��CM3=PM3����M3��2��
| 3 |
| 2 |
��PC=PM4����M4��2��-2
| 5 |
�����������ĵ�M�ֱ�ΪM1��2��7����M2��2��2
| 5 |
M3��2��
| 3 |
| 2 |
| 5 |
������������Ҫ���������������ε��ж��������Լ����������ε����ʺʹ���ϵ��������κ�������ʽ��֪ʶ�����÷������۵ó��ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
����
=
�Ľ�Ϊ��������
| 1 |
| x-1 |
| 2 |
| x+1 |
| A��-1 | B��1 | C��2 | D��3 |
 ��ͼ������ABCD�ı�AB=4��BC=3��һ���������������ھ���ABCD�ڣ����������ԲO��ֱ�����AB�غϣ���A����0�̶ȣ���B����180�̶ȣ�P�����������İ�Բ����һ���㣬��P����������BC��CD�������ӳ��ߣ��ֱ��ڵ�E��F�����P�Ŀ̶���Ϊn����PAB=����
��ͼ������ABCD�ı�AB=4��BC=3��һ���������������ھ���ABCD�ڣ����������ԲO��ֱ�����AB�غϣ���A����0�̶ȣ���B����180�̶ȣ�P�����������İ�Բ����һ���㣬��P����������BC��CD�������ӳ��ߣ��ֱ��ڵ�E��F�����P�Ŀ̶���Ϊn����PAB=����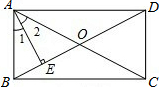 ��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AE��BD������ΪE����1=��2��AB=2cm��
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AE��BD������ΪE����1=��2��AB=2cm�� ���öԳƱ任����Ƴ�����ͼ������ͼ���ڷ���ֽ��ÿһ�����㶼�ڸ���ϵ��ı��Σ���ÿ��С�����εı߳���Ϊ1������������⣺
���öԳƱ任����Ƴ�����ͼ������ͼ���ڷ���ֽ��ÿһ�����㶼�ڸ���ϵ��ı��Σ���ÿ��С�����εı߳���Ϊ1������������⣺ ��ͼ���ڡ�ABC��DE��AC�Ĵ�ֱƽ���ߣ�AE=6cm����ABD���ܳ�Ϊ26cm�����ABC���ܳ�Ϊ
��ͼ���ڡ�ABC��DE��AC�Ĵ�ֱƽ���ߣ�AE=6cm����ABD���ܳ�Ϊ26cm�����ABC���ܳ�Ϊ