题目内容
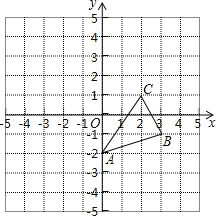
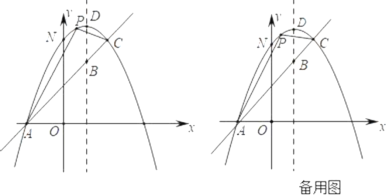
【题目】如图，抛物线
的对称轴为直线
，且抛物线经过
，
两点，与
轴交于点
.
（1）若直线
经过、
两点，求直线
和抛物线的解析式；
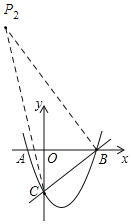
（2）设点
为抛物线上的一个动点，联结
、
，若
是以为直角边的直角三角形，求此时点的坐标；
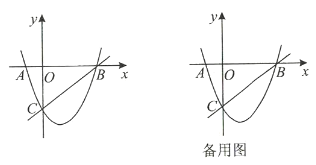
【答案】（1）
的解析式：
，抛物线解析式：
；（2）
，
【解析】
（1）根据对称轴及A点坐标得出B点坐标，从而得出直线BC解析式，再由A、B、C三点坐标得出抛物线解析式；（2）分别过B、C两点作BC的垂线，得出垂线的解析式，与抛物线解析式联立解出P点.
解：（1）∵对称轴为x=2，且抛物线经过A（-1，0），
∴B（5，0）．
把B（5，0），C（0，-5）分别代入y=mx+n得
，
解得：
，
∴直线BC的解析式为y=x-5．
设y=a（x-5）（x+1），把点C的坐标代入得：-5a=-5，解得：a=1，
∴抛物线的解析式为：y=x2-4x-5．
（2）①过点C作CP1⊥BC，交抛物线于点P1，如图，
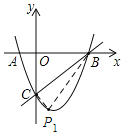
则直线CP1的解析式为y=-x-5，由
，
解得：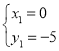
（舍去）；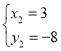
，
∴P1（3，-8）；
②过点B作BP2⊥BC，交抛物线于P2，如图，
则BP2的解析式为y=-x+5，由
，
解得：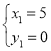
（舍去），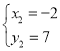
，
∴P2（-2，7）；
综上，，
练习册系列答案
相关题目
