Question

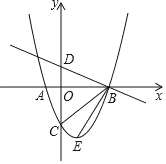
【题目】如图，抛物线y=ax2+bx﹣3，顶点为E，该抛物线与x轴交于A，B两点，与y轴交子点C，且OB=OC=3OA，直线y=﹣x+1与y轴交于点D．求∠DBC﹣∠CBE=_____．

Answer 1

【答案】45°．

【解析】

先求出点D、点C的坐标，得出点B、A的坐标，求出抛物线的解析式，得出抛物线的顶点坐标，根据勾股定理求出BC、CE、BE，由勾股定理的逆定理证明△BCE为直角三角形，∠BCE=90°，由三角函数证出∠DBO=∠CBE，即可得出∠DBC-∠CBE=∠DBC-∠DBO=∠OBC=45°．

将x=0代入y=x+1，y=1，

∴D（0，1），

将x=0代入y=ax2+bx-3得：y=-3，
∴C（0，-3），

∵OB=OC=3OA，

∴B（3，0），A（-1，0），∠OBC=45°，

对于直线y=x+1，

当y=0时，x=3，

∴直线y=x+1过点B．
将点C（0，-3）的坐标代入y=a（x+1）（x-3），

得：a=1，

∴抛物线的解析式为：y=x2-2x-3=（x-1）2-4，

∴抛物线y=x2-2x-3的顶点为E（1，-4）．

于是由勾股定理得：

BC=3，CE=，BE=2．

∵BC2+CE2=BE2，

∴△BCE为直角三角形，∠BCE=90°，

因此tan∠CBE==．

又tan∠DBO==，

则∠DBO=∠CBE，

∴∠DBC-∠CBE=∠DBC-∠DBO=∠OBC=45°．

故答案为：45°.