题目内容
【题目】已知如图,![]() 是直角三角形
是直角三角形![]() ,
,![]() ,
,![]() ,点
,点![]() 由点
由点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 由点
由点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,若
的速度运动,若![]() 、
、![]() 同时开始运动。
同时开始运动。
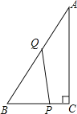
(1)运动多少秒时![]() 是直角三角形?
是直角三角形?
(2)运动多少秒时△![]() 的面积是
的面积是![]() 面积的
面积的![]() ?
?
(3)运动多少秒时![]() 的长度是
的长度是![]() ?
?
【答案】(1)![]() 或3时,
或3时,![]() 为直角三角形;(2)
为直角三角形;(2)![]() ;(3)
;(3)![]()
【解析】
先根据动点的速度、时间表示路程为:PC=t,BQ=2t,BP=6-2t,计算出走完全程的总时间为6秒,
(1)分两种情况:①当∠BQP=90°时,②当∠QPB=90°时,根据30°所对的直角边等于斜边的一半列式求出时间;
(2)作△PBQ的高线QD,根据含30°的直角三角形的性质得到QD=![]() t,利用△PBQ的面积是△ABC面积的
t,利用△PBQ的面积是△ABC面积的![]() 列式可求出t的值;
列式可求出t的值;
(3)在Rt△PQD中,根据勾股定理列方程:(![]() )2=(
)2=(![]() t)2+(6-2t)2,求出t的值,都符合题意.
t)2+(6-2t)2,求出t的值,都符合题意.
解:设运动时间为![]() 秒
秒
则![]()
![]()
![]()
![]()
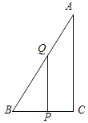
(1)如图:
![]()
![]()
![]()
![]()
![]()
![]()
②如图:

![]()
![]()
![]()
![]()
![]()
综上:![]() 或3时,
或3时,![]() 为直角三角形.
为直角三角形.
(2)过![]() 作
作![]() 于
于![]()
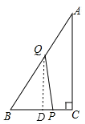
则![]()
![]()
![]()
![]()
![]()
![]()
整理得:![]()
![]()
![]()
(3)![]()
![]()
![]()
在![]() 中
中
![]()
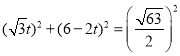
整理得:![]()
![]()
![]()

练习册系列答案
相关题目