题目内容
(1)计算题:(-3)0-
+|1-
|-(-1)-2;
(2)解方程:x2-2x=2x+1.
| 12 |
| 3 |
(2)解方程:x2-2x=2x+1.
考点:实数的运算,零指数幂,负整数指数幂,解一元二次方程-配方法
专题:计算题
分析:(1)原式第一项利用零指数幂法则计算,第二项化为最简二次根式,第三项利用绝对值的代数意义化简,最后一项利用负指数幂法则计算即可得到结果;
(2)方程变形后,利用公式法求出解即可.
(2)方程变形后,利用公式法求出解即可.
解答:解:(1)原式=1-2
+
-1-1
=-
-1;
(2)整理原方程,得:x2-4x-1=0,
这里a=1,b=-4,c=-1,
∵△=16+4=20,
∴x=
=2±
,
则x1=2+
,x2=2-
.
| 3 |
| 3 |
=-
| 3 |
(2)整理原方程,得:x2-4x-1=0,
这里a=1,b=-4,c=-1,
∵△=16+4=20,
∴x=
4±2
| ||
| 2 |
| 5 |
则x1=2+
| 5 |
| 5 |
点评:此题考查了实数的运算,以及解一元二次方程-配方法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知3是关于x的方程2x-a=1的解,则a的值为( )
| A、-5 | B、5 | C、7 | D、-7 |
 AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么? 开学后,某校学生部将学生《寒假做家务情况反馈表》收集整理,随机抽查了部分学生的反馈表,并分等级绘制成如图的统计图,请根据图中的信息回答下列问题:
开学后,某校学生部将学生《寒假做家务情况反馈表》收集整理,随机抽查了部分学生的反馈表,并分等级绘制成如图的统计图,请根据图中的信息回答下列问题: 已知:EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由.
已知:EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由.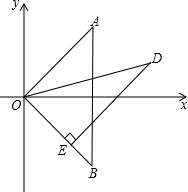 如图,等腰直角△OAB的直角顶点O是坐标原点,顶点在一、三象限的角平分线上,顶点B在第四象限,Rt△ODE的直角顶点E在直线OB上,且OD=4,∠ODE=30°,将Rt△ODE绕点O顺时针旋转15°,得到Rt△OD1E1,线段D1E1交直线OB于点F.若某反比例函数的图象经过点F,则这个反比例函数的解析式为
如图,等腰直角△OAB的直角顶点O是坐标原点,顶点在一、三象限的角平分线上,顶点B在第四象限,Rt△ODE的直角顶点E在直线OB上,且OD=4,∠ODE=30°,将Rt△ODE绕点O顺时针旋转15°,得到Rt△OD1E1,线段D1E1交直线OB于点F.若某反比例函数的图象经过点F,则这个反比例函数的解析式为