题目内容
 AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?解:BE∥DF.
∵AB⊥BC,
∴∠ABC=
即∠3+∠4=
又∵∠1+∠2=90°,
且∠2=∠3,
∴
理由是:
∴BE∥DF.
理由是:
考点:平行线的判定
专题:推理填空题
分析:由AB垂直于BC,利用垂直的定义得到∠ABC为直角,进而得到∠3与∠4互余,再由∠1与∠2互余,根据∠2=∠3,利用等角的余角相等得到∠1=∠4,利用同位角相等两直线平行即可得证.
解答:解:BE∥DF,
∵AB⊥BC,
∴∠ABC=90°,
即∠3+∠4=90°.
又∵∠1+∠2=90°,
且∠2=∠3,
∴∠1=∠4,
理由是:等角的余角相等,
∴BE∥DF.
理由是:同位角相等,两直线平行.
故答案为:90;90;∠1,∠4;等角的余角相等;同位角相等,两直线平行.
∵AB⊥BC,
∴∠ABC=90°,
即∠3+∠4=90°.
又∵∠1+∠2=90°,
且∠2=∠3,
∴∠1=∠4,
理由是:等角的余角相等,
∴BE∥DF.
理由是:同位角相等,两直线平行.
故答案为:90;90;∠1,∠4;等角的余角相等;同位角相等,两直线平行.
点评:此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
某市有近4万名考生参加中考,为了解这些考生的数学成绩,从中抽取1500名考生的数学成绩进行统计分析,以下说法正确的是( )
| A、这1500名考生是总体的一个样本 |
| B、近4万名考生是总体 |
| C、其中每位考生的数学成绩是个体 |
| D、1500名学生是样本容量 |
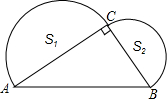 如图,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2.
如图,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2.