题目内容
 如图,A、B、C都是⊙O上的点,
如图,A、B、C都是⊙O上的点, |
| AC |
 |
| BC |
考点:圆心角、弧、弦的关系,全等三角形的判定与性质
专题:证明题
分析:由
=
,可得∠AOC=∠BOC,又由CD⊥OA,CE⊥OB,易证得△ODC≌△OEC,即可证得OD=OE.
 |
| AC |
 |
| BC |
解答:证明:∵
=
,
∴∠AOC=∠BOC,
又∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°,
在△ODC和△OEC中,
,
∴△ODC≌△OEC(AAS),
∴OD=OE.
 |
| AC |
 |
| BC |
∴∠AOC=∠BOC,
又∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°,
在△ODC和△OEC中,
|
∴△ODC≌△OEC(AAS),
∴OD=OE.
点评:此题考查了弧与圆心角的关系以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图,笑脸盖住的点的坐标可能是( )
如图,笑脸盖住的点的坐标可能是( )| A、(5,2) |
| B、(-2,3) |
| C、(3,-4) |
| D、(-4,-6) |
 我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.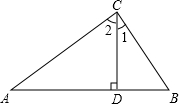 如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是
如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是 如图,在直角梯形ABCD中,AB∥DC,∠A=90°,若DC=3cm,AB=9cm,则此梯形的中位线长为
如图,在直角梯形ABCD中,AB∥DC,∠A=90°,若DC=3cm,AB=9cm,则此梯形的中位线长为 如图所示,△ABC的顶点A(-3,2),B(-4,0),C(-1,0).
如图所示,△ABC的顶点A(-3,2),B(-4,0),C(-1,0).