题目内容
14．若方程组$\left\{\begin{array}{l}{3x+y=k+1}\\{x+3y=3}\end{array}\right.$的解x，y满足0＜x+y＜1，则k的取值范围是-4＜k＜0．分析 方程组两方程相加表示出x+y，代入已知不等式求出k的范围即可．
解答 解：$\left\{\begin{array}{l}{3x+y=k+1①}\\{x+3y=3②}\end{array}\right.$，
①+②得：4（x+y）=k+4，即x+y=$\frac{k+4}{4}$，
代入已知不等式得：0＜$\frac{k+4}{4}$＜1，
解得：-4＜k＜0，
故答案为：-4＜k＜0
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
练习册系列答案
相关题目
4．把分式$\frac{{x}^{2}-3x}{{x}^{2}-9}$进行约分，其结果是（ ）
| A． | $\frac{x}{x-3}$ | B． | $\frac{x}{x+3}$ | C． | $\frac{x}{x-9}$ | D． | $\frac{x-3}{x+3}$ |
2．已知正多边形的一个外角等于60°，则该正多边形的边数为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
9．下列计算正确的是（ ）
| A． | a2•a3=a6 | B． | a2-b2=（a-b）2 | C． | （3b3）2=6b6 | D． | （-a）5÷（-a）3=a2 |
+1是一个完全平方式，但是其中一项看不清了，你认为这一项应该是$\frac{1}{16{x}^{2}}$，4x，-4x，4x4（写出所有你认为正确的答案）．
6．在Rt△ABC中，∠C=90°，下列式子中不一定成立的是（ ）
| A． | cosA=sinB | B． | sinA=cosB | C． | sin（A+B）=sinC | D． | sinA=sinB |
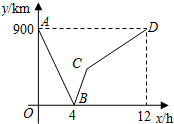一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象解决以下问题：