题目内容
已知（a+b）2=7，（a-b）2=3．
（1）求a2+b2、ab的值；
（2）求a4+b4的值．
（1）求a2+b2、ab的值；
（2）求a4+b4的值．
考点：完全平方公式
专题：
分析：（1）先根据完全平方公式展开，再相加或相减即可得出答案；
（2）根据完全平方公式变形，再整体代入求出即可．
（2）根据完全平方公式变形，再整体代入求出即可．
解答：解：（1）由题意得：a2+2ab+b2①，a2-2ab+b2②，
①+②，得：a2+b2=5，
①-②，得：ab=1；
（2）a4+b4
=（a2+b2）2-2（ab）2
=52-2×12
=23．
①+②，得：a2+b2=5，
①-②，得：ab=1；
（2）a4+b4
=（a2+b2）2-2（ab）2
=52-2×12
=23．
点评：本题考查了完全平方公式的应用，注意：完全平方公式有（a+b）2=a2+2ab+b2，（a-b）2=a2-2ab+b2．
练习册系列答案
相关题目
如果|a+2|与（b-1）2互为相反数，那么代数式（a+b）2011的值是（ ）
| A、1 | B、-1 | C、±1 | D、2008 |
已知n表示正整数，则
+
=（ ）
| 1n |
| 2 |
| (-1)n |
| 2 |
| A、0 | B、1 |
| C、0或1 | D、无法确定，随n值的不同而不同 |
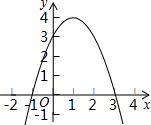已知二次函数y=-x2+2x+k+2与x轴的公共点有两个．求：