题目内容

13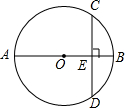．AB为⊙O的直径，弦CD⊥AB于点E，已知CD=16，OE=6，则⊙O的直径为（　　）
A．8B．10C．16D．20

分析 连接OC，根据垂径定理求出CE，根据勾股定理求出OC即可．

解答 解：连接OC，
∵AB为⊙O的直径，弦CD⊥AB于点E，CD=16，
∴CE=DE=$\frac{1}{2}$CD=8，∠OEC=90°，
在Rt△OEC中，由勾股定理得：OC=$\sqrt{O{E}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10，
所以⊙O的直径为20，
故选D．

点评 本题考查了勾股定理和垂径定理等知识点，能根据垂径定理求出CE的长是解此题的关键，注意：垂直于弦的直径平分这条弦．

练习册系列答案
相关题目
3．数轴上与-1距离3个长度的点表示的数是-4或2．
4．以直线AB上一点O为端点作射线 OC，使∠BOC=60°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE=90°）
（1）如图1，若直角三角板DOE的一边OD放在射线OB上，则∠COE=30°；
（2）如图2，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OE恰好平分∠AOC，请说明OD所在射线是∠BOC的平分线；
（3）如图3，将三角板DOE绕点O逆时针转动到某个位置时，若恰好∠COD=$\frac{1}{5}$∠AOE，求∠BOD的度数？
1．王师傅打算制作一个正方体木箱，其体积是3.375m3，试间：
（1）该正方体木箱的棱长是多少？
（2）所用木板面积是多少？
8．在直角坐标系中，点A（m，1）与点B（-3，n）关于x轴对称，则m+n=-4．
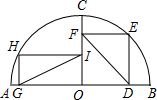18．如图，C是以点O为圆心，AB为直径的半圆上一点，且CO⊥AB，在OC两侧分别作矩形OGHI和正方形ODEF，且点I，F在OC上，点H，E在半圆上，可证：IG=FD．小云发现连接图中已知点得到两条线段，便可证明IG=FD．
请回答：小云所作的两条线段分别是OH和OE；
证明IG=FD的依据是矩形的对角线相等，同圆的半径相等和等量代换．
5．下列个数中，无理数是（　　）
A．0B．0.1010010001C．$\sqrt{3}$D．-$\frac{1}{3}$
2．在△ABC与△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，延长DE交BC于点F，连接DC，BE．
（1）如图1，当点B，A，D在同一直线上时，且∠ABE=30°，AE=2，求BF的长．
（2）如图2，当∠BEA=90°时，求证：BF=CF．
（3）如图3，当点E在∠ABC的平分线上时，BE交DC于点G，请直接写出EG、DG、CG之间的数量关系．
3．下列各组中的两项是同类项的是（　　）
A．3a2b与ab2B．a2b与ba2C．3ab与aD．2与3x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网