题目内容
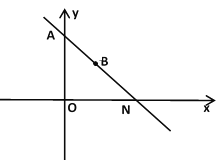
【题目】若直线y=kx+b过A(0,2)和点B(1,1)，与x轴交于点N.
(1)直线的表达式为_________.
(2)在直线AB上有一点M(0.5，a)，点Q是x轴上一个动点，若直线MQ把△AON的面积分成1:4两部分，求Q坐标.
【答案】（1）
（2）（
，0）或（
，0）
【解析】
（1）已知直线
过A(0,2)和点B(1,1)两点，则可把两点坐标带入直线方程，求出k和b，再次代入得到直线的表达式.
（2）先根据方程求出点M、N的坐标，再在ON之间标出点Q（x，0），连接MQ. 因为直线MQ把△AON的面积分成1:4两部分，所以△MQN与△AON的面积之比为1：5，然后写出方程，求x，即可知道Q点的坐标.
（1）分别把
、
与
、
带入直线方程中，得到方程组
解得
，则直线方程的表达式为
.
（2）①根据表达式得到N（2,0）和M（0.5,1.5），
，.设 Q（x，0），则
，连接MQ，作MP垂直于x轴（MP是△MQN的高），如图所示：
则
.因为直线MQ把△AON的面积分成1:4两部分，所以△MQN与△AON的面积之比为1：5.
，
，解得
，则Q（
，0）
②如图所示，设 Q（a，0），C（0，c），则AC=2-c，作DM垂直于AC，则MD为三角形ACM的高.由①知
，解得c=
.
设QM的解析式为y=kx+b，代入C（0，），M（0.5,1.5），则直线QM的解析式为：
求a的值，则令y=0，得a=，则Q（，0）
练习册系列答案
相关题目
