Question

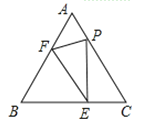
【题目】以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连结BE、CF.

（1）你能找到哪两个图形可以通过旋转而相互得到，并指出旋转中心和旋转角.

（2）试探索BE和CF有什么数量关系和位置关系？并说明理由.

Answer 1

【答案】(1) 三角形ABE 与三角形ACF ，旋转中心为点A，旋转角度为90°或270°(2) BE=CF且BE⊥CF，理由详见解析.

【解析】

（1）旋转不改变图形的大小，则一定找全等图形，由SAS条件可证明全等的图形可以是三角形ACF与三角形ABE，三角形ABE以点A顺时针旋转90°可得到三角形ACF.

（2）由三角形ACF与三角形ABE全等得到BE和CF相等，再通过直角三角形中锐角的等量代换得到 FHB=90°，进而得到BE和CF垂直.

（1）∵四边形ACDE和四边形ABGF是正方形

∴AB=AF，AC=AE

又∠FAB=∠EAC=90°

∴∠FAB+∠BAC=∠EAC+∠BAC

即∠FAC=∠EAB

在三角形ACF与三角形AEB中

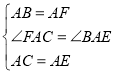
所以 (SAS)

由旋转不改变图形的大小可知，三角形ABE绕点A顺时针旋转90°可得到三角形ACF.

三角形ABE绕点A逆时针旋转270°可得到三角形ACF.

（2）判断BE=CF且BE⊥CF，理由如下：

由（1）可知

则BE=CF，∠ACF=∠AEB

在直角三角形AOE中，∠AEO+∠AOE=90°

而∠AOE=∠COH

则在三角形HOC中，∠ACH+∠COH=90°

即三角形HOC是直角三角形

则∠OHC=90°

即BE⊥CF

综上：BE=CF且BE⊥CF