Question

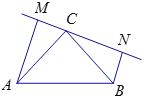
【题目】如图，在直角△BAD中延长斜边BD到点C，使，若，则的值为（ ）

A. B. C. D.

Answer 1

【答案】D

【解析】

延长AD，过点C作CE⊥AD的延长线，垂足为点E，由tanB=，得到AD:AB=5:3，可设AD=5x，则AB=3x；

证明△CDE∽△BDA，然后根据相似三角形的对应边成比例可用x表示出DE、CE、AE的长，最后根据正切的定义解答

如图，延长AD，过点C作CE⊥AD，垂足为E，

∵tanB=，

即AD:AB=5:3，

∴设AD=5x，则AB=3x.

∵∠CDE=∠BDA，∠CED=∠BAD，

∴△CDE∽△BDA，

∴CE:AB=DE:AD=CD:BD=1:2，

∴CE=x，DE=x，

∴AE=x，

∴tan∠CAD= =.

故选D.