题目内容
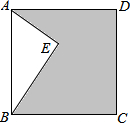 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=5.BE=12,则阴影部分的面积是( )
如图,点E在正方形ABCD内,满足∠AEB=90°,AE=5.BE=12,则阴影部分的面积是( )| A、39 | B、69 |
| C、139 | D、169 |
考点:勾股定理,正方形的性质
专题:
分析:根据勾股定理求出AB,分别求出△AEB和正方形ABCD的面积,即可求出答案.
解答:解:∵在Rt△AEB中,∠AEB=90°,AE=5,BE=12,由勾股定理得:AB=13,
∴正方形的面积是13×13=169,
∵△AEB的面积是
AE×BE=
×5×12=30,
∴阴影部分的面积是169-30=139,
故选C.
∴正方形的面积是13×13=169,
∵△AEB的面积是
| 1 |
| 2 |
| 1 |
| 2 |
∴阴影部分的面积是169-30=139,
故选C.
点评:本题考查了正方形的性质,三角形的面积,勾股定理的应用,主要考查学生的计算能力和推理能力.

练习册系列答案
相关题目
某次数学竞赛活动,共有16个选择题.评分标准为:答对一题得6分,答错一题扣2分,不答题不得分也不扣分.某同学有一道题未答,那么这个同学至少答对( )道题,成绩才能达到60分以上?
| A、10道 | B、11道 |
| C、12道 | D、13道 |
下列各对数中,互为倒数的是( )
| A、2与-2 | ||
B、-2与-
| ||
C、2与-
| ||
D、-2与
|
已知
=0,则x为( )
| x+3 |
| A、x>-3 | B、x<-3 |
| C、x=-3 | D、x的值不能确定 |
 如图,在抛物线y=-x2上有A,B两点,其横坐标分别为1,2;在y轴上有一动点C,则AC+BC最短距离为( )
如图,在抛物线y=-x2上有A,B两点,其横坐标分别为1,2;在y轴上有一动点C,则AC+BC最短距离为( )| A、5 | ||
B、3
| ||
C、
| ||
D、2
|
 如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=40°,则∠2=
如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=40°,则∠2= 如图所示,将矩形纸片ABCD按如图方式折叠,EF、EC为折痕,折叠后点A落在边CD的A处,点B落在边A′E的B′处.若A′D=4,BC=8,则AE的长是( )
如图所示,将矩形纸片ABCD按如图方式折叠,EF、EC为折痕,折叠后点A落在边CD的A处,点B落在边A′E的B′处.若A′D=4,BC=8,则AE的长是( ) 将等腰Rt△ABC和等腰Rt△DEF如图摆放,P、M、N是AD、BE、CF的中点,求证:PM=PM且PM⊥PN.
将等腰Rt△ABC和等腰Rt△DEF如图摆放,P、M、N是AD、BE、CF的中点,求证:PM=PM且PM⊥PN.