题目内容
1．已知圆锥的底面半径为2cm，母线长为9cm，则圆锥的侧面展开图的圆心角是80°．分析 圆锥的侧面展开图是扇形，圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长，利用弧长公式即可求解．
解答 解：设圆锥的侧面展开图的圆心角是n°，
由题意得$\frac{n×π×9}{180}$=2×π×2，
解得n=80．
故答案为80．
点评 本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
相关题目
11．
如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD等于（ ）
如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD等于（ ）| A． | 57.5° | B． | 65° | C． | 115° | D． | 130° |
12．已知一个样本含有30个数据，这些数据被分成4组，各组数据的个数之比为2：4：3：1，则第三小组的频数和频率分别为（ ）
| A． | 12、0.3 | B． | 9、0.3 | C． | 9、0.4 | D． | 12、0.4 |
9．
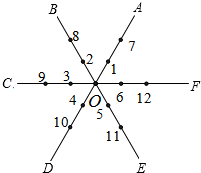如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…，则数字“2016”在（ ）
如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…，则数字“2016”在（ ）| A． | 射线OA上 | B． | 射线OB上 | C． | 射线OD上 | D． | 射线OF上 |
16．一只不透明的袋子中装有1个黑球3个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到白球的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
如图，在△ABC中，∠ABC=120°，⊙O是△ABC的外接圆，点P是$\widehat{AmC}$上的一个动点．