题目内容
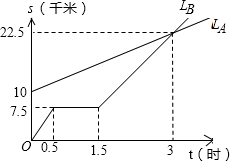
 如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距
10
10
千米.(2)走了一段路后,自行车发生故障,进行修理,所用的时间是
1
1
小时.(3)B出发后
3
3
小时与A相遇.(4)若B的自行车不发生故障,保持出发时的速度前进,
| 12 |
| 13 |
| 12 |
| 13 |
分析:(1)还没出发时两人之间的距离也就是B出发时与A的距离;
(2)发生故障时行驶的路程不发生变化,求出两时间的差即可;
(3)根据图象,3小时时两人的路程相同,即为相遇点;
(4)先求出两人的速度,再根据相遇时B比A多走10千米列出方程求解即可.
(2)发生故障时行驶的路程不发生变化,求出两时间的差即可;
(3)根据图象,3小时时两人的路程相同,即为相遇点;
(4)先求出两人的速度,再根据相遇时B比A多走10千米列出方程求解即可.
解答:解:(1)由图可知,B出发时与A相距10千米;
(2)B修理自行车所用的时间为:1.5-0.5=1小时;
(3)3小时时两人的路程都是22.5千米,
所以,B出发后3小时与A相遇;
(4)出发时A的速度为:
=
千米/时,
B的速度为:
=15千米/时,
设若B的自行车不发生故障,保持出发时的速度前进,x小时与A相遇,
根据题意得,15x-
x=10,
解得x=
.
故答案为:(1)10;(2)1;(3)3;(4)
.
(2)B修理自行车所用的时间为:1.5-0.5=1小时;
(3)3小时时两人的路程都是22.5千米,
所以,B出发后3小时与A相遇;
(4)出发时A的速度为:
| 22.5-10 |
| 3 |
| 25 |
| 6 |
B的速度为:
| 7.5 |
| 0.5 |
设若B的自行车不发生故障,保持出发时的速度前进,x小时与A相遇,
根据题意得,15x-
| 25 |
| 6 |
解得x=
| 12 |
| 13 |
故答案为:(1)10;(2)1;(3)3;(4)
| 12 |
| 13 |
点评:本题考查了利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,以及追击问题的等量关系是解题的关键.

练习册系列答案
相关题目
 如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.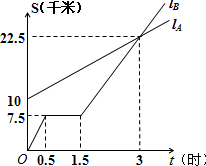 如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系. 如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间的关系.
如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间的关系.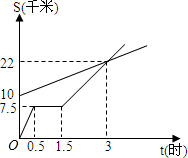 如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.