题目内容
在进行二次根式化简时,我们有时会碰上如| 5 | ||
|
|
| 2 | ||
|
| 5 | ||
|
5×
| ||||
|
| 5 |
| 3 |
| 3 |
|
|
| ||
| 3 |
| 2 | ||
|
2×(
| ||||
(
|
2(
| ||
(
|
| 3 |
| 2 | ||
|
| 2 | ||
|
| 3-1 | ||
|
(
| ||
|
(
| ||||
|
| 3 |
以上这种化简的方法叫做分母有理化.
(1)请化简
| 2 | ||||
|
(2)若a是
| 2 |
| 3 |
| a |
(3)矩形的面积为3
| 5 |
| 5 |
(4)化简
| 2 | ||
1+
|
| 2 | ||||
|
| 2 | ||||
|
| 2 | ||||
|
分析:(1)分子、分母同乘以最简有理化因式
-
,化简即可;
(2)由题意可得a=
-1,代入分母有理化即可.
(3)首先求另一边长为:
,化简再按矩形的周长公式解答;
(4)把各加数分母有理化,再加减即可.
| 5 |
| 3 |
(2)由题意可得a=
| 2 |
(3)首先求另一边长为:
3
| ||
|
(4)把各加数分母有理化,再加减即可.
解答:解:(1)
=
=
-
,
故答案为:
-
;
(2)∵
<
<
,a是
的小数部分,
∴a=
-1,
∴
=
=3
+3.
故答案为:3
+3;
(3)另一边长为:
=
=17+7
,
周长为:2(17+7
+
-2)=30+16
,
故答案为:30+16
;
(4)
+
+
+…+
=
+
+
+…+
=
=
.
| 2 | ||||
|
2(
| ||||||||
(
|
| 5 |
| 3 |
故答案为:
| 5 |
| 3 |
(2)∵
| 1 |
| 2 |
| 4 |
| 2 |
∴a=
| 2 |
∴
| 3 |
| a |
| 3 | ||
|
| 2 |
故答案为:3
| 2 |
(3)另一边长为:
3
| ||
|
(3
| ||||
(
|
| 5 |
周长为:2(17+7
| 5 |
| 5 |
| 5 |
故答案为:30+16
| 5 |
(4)
| 2 | ||
1+
|
| 2 | ||||
|
| 2 | ||||
|
| 2 | ||||
|
=
2(
| ||
| 5-1 |
2(
| ||||
| 9-5 |
2(
| ||||
| 13-9 |
2(
| ||||
| (4n+1)-(4n-3) |
=
| ||||||||||||||
| 2 |
=
| ||
| 2 |
点评:此题考查分母有理化,分母有理化是化简二次根式的一种重要方法.分母有理化时,应结合题目的具体特点,选择适当的方法.

练习册系列答案
相关题目
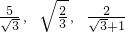 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: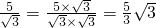 (一),
(一),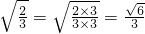 (二),
(二),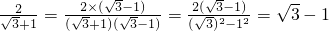 (三),
(三),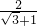 还可以用以下方法化简:
还可以用以下方法化简: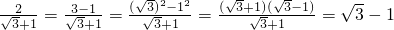 (四)
(四)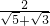 .
.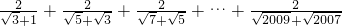 .
.