题目内容
阅读与解答:
在进行二次根式化简时,我们有时会碰上如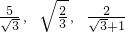 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: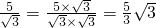 (一),
(一),
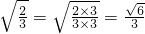 (二),
(二),
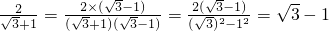 (三),
(三),
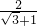 还可以用以下方法化简:
还可以用以下方法化简: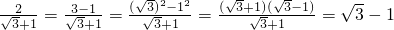 (四)
(四)
以上这种化简的方法叫做分母有理化.
(1)请用不同的方法化简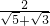 .
.
①参照(三)式得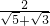 =______.
=______.
②参照(四)式得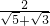 =______.
=______.
(2)化简: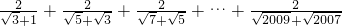 .
.
解:(1)①原式= =
= =
= .
.
②原式= =
= =
= .
.
故应填 .
.
(2)原式=2 +
+
+
=
=
= .
.
故应填 .
.
分析:解答本题要认真阅读前面的分析,根据题目的要求选择正确的解题方法.
点评:主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.
 =
= =
= .
.②原式=
 =
= =
= .
.故应填
 .
.(2)原式=2
 +
++

=

=

=
 .
.故应填
 .
.分析:解答本题要认真阅读前面的分析,根据题目的要求选择正确的解题方法.
点评:主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
相关题目
 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: (一),
(一), (二),
(二), (三),
(三), 还可以用以下方法化简:
还可以用以下方法化简: (四)
(四) .
. =______
=______ 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: (一),
(一), (二),
(二), (三),
(三), 还可以用以下方法化简:
还可以用以下方法化简: (四)
(四) .
. =______
=______