题目内容
如图，E为平行四边形ABCD的边BC延长线上一点，连结AE，交边CD于点F．在不添加辅助线的情况下，则有考点：相似三角形的判定
专题：
分析：先根据平行四边形的性质得AD∥BC，AB∥CD，△ABC∽△CD，再利用平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似可判断△ADF∽△ECF，△ECF∽△EBA，则△ADF∽△EBA．
解答：解：∵四边形ABCD为平行四边形，
∴AD∥BC，AB∥CD，△ABC∽△CD，
∴△ADF∽△ECF，△ECF∽△EBA，
∴∴△ADF∽△EBA，
即图中共有4对相似三角形．
故答案为4．
∴AD∥BC，AB∥CD，△ABC∽△CD，
∴△ADF∽△ECF，△ECF∽△EBA，
∴∴△ADF∽△EBA，
即图中共有4对相似三角形．
故答案为4．
点评：本题考查了相似三角形的判定：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；有两组角对应相等的两个三角形相似．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
如图，⊙O是正三角形ABC的外接圆，点P在劣弧AB上，∠ABP=23°，则∠BCP=
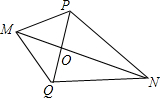如图，MP=MQ，PN=QN，MN交PQ于点O，则下列结论不正确的是（ ）| A、MQ=NO |
| B、OP=OQ |
| C、△MPN≌△MQN |
| D、∠MPN=∠MQN |
下列各组线段能组成一个三角形的是（ ）
| A、3cm，3cm，6cm |
| B、2cm，3cm，6cm |
| C、5cm，8cm，12cm |
| D、4cm，7cm，11cm |
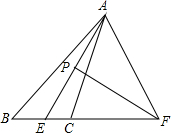AE是∠BAC的平分线，AE的中垂线PF交BC的延长线于点F，若AE=AF，∠CAF=30°，则∠B=
如图，从电线杆离地面8米处向地面拉一条缆绳，这条缆绳在地面上的固定点距离电线杆底部15米，则这条缆绳的长为