题目内容
在平面直角坐标系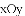
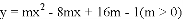 与
与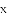
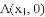 ,
,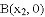 .
.
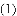
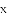
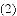
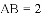
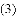
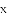
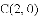
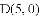
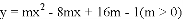 与线段
与线段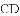
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
题目内容
在平面直角坐标系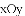
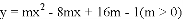 与
与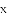
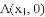 ,
,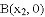 .
.
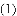
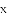
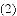
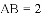
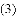
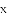
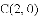
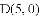
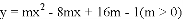 与线段
与线段
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案