题目内容
20.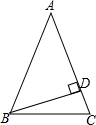 如图,在△ABC中,AB=AC,BD⊥AC,垂足为点D.若∠BAC=30°,则∠DBC的度数为15°.
如图,在△ABC中,AB=AC,BD⊥AC,垂足为点D.若∠BAC=30°,则∠DBC的度数为15°.
分析 本题可根据等腰三角形的性质和三角形内角和定理求出∠C的度数,然后在Rt△DBC中,求出∠DBC的度数.
解答 解:∵在△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB=(180°-30°)÷2=75°;
又∵BD⊥AC垂足为D,
∴∠DBC=90°-∠ACB=90°-75°=15°.
故答案为:15.
点评 要考查了三角形的内角和外角之间的关系以及等腰三角形的性质.
(1)三角形的外角等于与它不相邻的两个内角和.
(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.注意:本题中可简单的利用同角的余角相等这一性质解题.垂直和直角总是联系在一起.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
10.解不等式组并求它的整数解.
$\left\{\begin{array}{l}\frac{x-8}{3}<0\\ 1-\frac{1}{2}x≤-\frac{1}{3}x\end{array}$.
$\left\{\begin{array}{l}\frac{x-8}{3}<0\\ 1-\frac{1}{2}x≤-\frac{1}{3}x\end{array}$.
11. 如图所示物体的左视图为( )
如图所示物体的左视图为( )
 如图所示物体的左视图为( )
如图所示物体的左视图为( )| A. |  | B. |  | C. |  | D. |  |
15. 如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )
如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )
 如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )
如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )| A. | -1<x≤1 | B. | -1<x<1 | C. | x>-1 | D. | x≤1 |
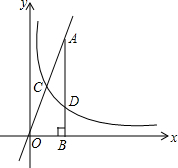 如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,8)作AB垂直于x轴于点B,交反比例函数图象于点D,且AD=3BD.
如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,8)作AB垂直于x轴于点B,交反比例函数图象于点D,且AD=3BD.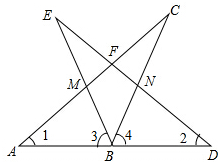 如图,已知△ABC和△BDE,B为AD中点,BE=BC,∠1=∠2,∠3=∠4,请根据题意,写出图中的两对全等三角形:△ABM≌△DBN,△ABC≌△DBE.
如图,已知△ABC和△BDE,B为AD中点,BE=BC,∠1=∠2,∠3=∠4,请根据题意,写出图中的两对全等三角形:△ABM≌△DBN,△ABC≌△DBE.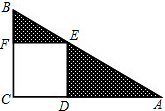 如图所示,在△ABC中,∠ACB=90°,正方形CDEF的顶点E在斜边AB上,且AE=5,BE=8,则△ADE与△BEF的面积和为1780.
如图所示,在△ABC中,∠ACB=90°,正方形CDEF的顶点E在斜边AB上,且AE=5,BE=8,则△ADE与△BEF的面积和为1780.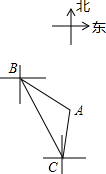 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.