题目内容
8.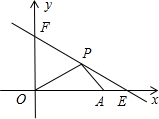 已知:如图,直线y=kx+b与x轴y轴分别交于点E,F,点E,F的坐标为(8,0),(0,6),点A的坐标为(6,0).
已知:如图,直线y=kx+b与x轴y轴分别交于点E,F,点E,F的坐标为(8,0),(0,6),点A的坐标为(6,0).(1)求直线EF的函数关系式;
(2)若点P(x,y)是第一象限内的直线y=kx+b上的一个动点,当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,△OPA的面积为9,并说明理由.
分析 (1)将点E、F的坐标代入直线y=kx+b中得出关于k、b的二元一次方程,解方程即可得出结论;
(2)过点P作PD⊥x轴于点D,由P点在第一象限可得出0<x<8,再根据坐标系中点的坐标的意义可知线段OA、PD的长度,结合三角形的面积公式即可得出结论;
(3)令S=9,得出关于x的一元一次方程,解方程求出x的值,根据E、F点横坐标的数值即可得知此事点P为线段EF的中点.
解答 解:(1)∵点E(8,0),点F(0,6)在直线EF上,
∴有$\left\{\begin{array}{l}{0=8k+b}\\{6=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=6}\end{array}\right.$.
∴直线EF的函数关系式为y=-$\frac{3}{4}$x+6.
(2)过点P作PD⊥x轴于点D,如图所示.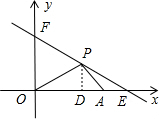
∵点P(x,y)是第一象限内的直线y=kx+b上的点,
∴y=-$\frac{3}{4}$x+6,且0<x<8.
∵点A的坐标为(6,0),点P的坐标为(x,-$\frac{3}{4}$x+6),
∴OA=6,PD=-$\frac{3}{4}$x+6.
△OPA的面积S=$\frac{1}{2}$OA•PD=$\frac{1}{2}$×6(-$\frac{3}{4}$x+6)=-$\frac{9}{4}$x+18(0<x<8).
(3)令S=9,即-$\frac{9}{4}$x+18=9,
解得:x=4,
∵E点横坐标为8,F点横坐标为0,
∴此时P点为线段EF的中点.
故当P运动到线段EF的中点时,△OPA的面积为9.
点评 本题考查了待定系数法求函数解析式、坐标系中点的意义、三角形的面积公式以及解一元一次方程,解题的关键是:(1)待定系数法求函数解析式;(2)找出OA、PD的长;(3)由S=9得出关于x的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,由点在函数图象上,代入点的坐标利用待定系数法即可求得函数解析式.

| A. | 696×103千米 | B. | 6.96×105千米 | C. | 6.96×106千米 | D. | 0.696×106千米 |

 B.
B.  C.
C.  D.
D. 
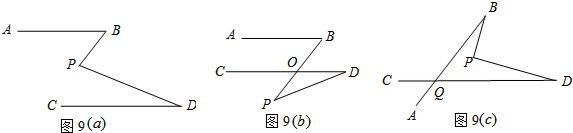
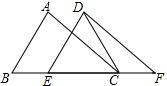 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为4.
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为4. 如图,△ABC沿着由点B到点E的方向,平移2cm到△DEF,已知BC=5cm,那么EC的长度为( )cm.
如图,△ABC沿着由点B到点E的方向,平移2cm到△DEF,已知BC=5cm,那么EC的长度为( )cm.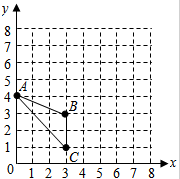 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.